2. 河北省数据科学与应用重点实验室, 河北 唐山 063009
2. Key Laboratory of Data Science and Application of Hebei Province, Tangshan Hebei 063009, China
LI Mingxia, born in 1992, M. S. candidate. Her research interests include rough set, interval concept lattice.
LIU Baoxiang, born in 1957, professor. His research interests include fuzzy control, concept lattice, data mining.
ZHANG Chunying, born in 1969, Ph. D., professor. Her research interests include concept lattice, artificial intelligence, multi-relational data mining.
概念格[1-3]是根据数据集中对象与属性之间的二元关系建立的一种概念层次结构, 是进行数据挖掘和知识处理的有效工具。概念格的每个节点是一个形式概念, 由外延(概念所覆盖的实例)和内涵(概念覆盖实例的共同特征)共同构成, 反映了概念内涵和外延的统一, 并且节点之间的关系体现了概念的泛化和特化关系, 因此概念格适合作为进行规则挖掘的基础性数据结构。在粗糙概念格[4-5]中, 利用粗糙集中的上、下近似理论, 描述具有部分属性的概念。如果形式背景过于稀疏, 可能会存在大量仅具备内涵中一个属性的对象, 由此构建的关联规则支持度和可信度都将大幅降低。区间概念格是经典概念格的扩展, 其概念外延是具备一定数量或比例的内涵中属性的对象集合, 即在区间范围[α, β]内满足内涵属性的对象集合, 区间概念格中概念度量的精度和覆盖度的定义在文献[6]中已经给出。
在构建区间概念格[7]、挖掘关联规则之前, 首先要确定区间参数的取值。之前的研究中, 构建的参数优化模型[8]主要的评价标准是在最优区间参数下格结构趋于稳定, 即当区间参数等步长变化到最优参数时, 格结构的更新度趋于零, 并且在该参数基础上挖掘得到的关联规则的数目适中且精度较高。后续的研究建立在三支决策空间[9]的基础上, 最优参数的评价标准为在由区间概念格构建的三支决策空间的基础上帮助用户作出拒绝和接收的决策而非不承诺。但是这些区间参数优化模型都没有考虑到格结构中概念节点冗余、数据量暴涨的缺点, 因此约简概念格, 提高关联规则的提取效率成为了另一个重要研究课题。文献[10]在形式背景的基础上构建可辨识属性矩阵实现对构建的概念格属性的约简;文献[11]从拓扑的角度研究了形式背景的属性约简问题, 提出了一种新约简的定义, 在保持属性概念外延的交不变的情况下给出了交协调集的判定定理, 从而实现对概念格的约简。这些方法都是建立在格结构已知的基础上, 对属性和节点进行分析以达到约简的目的。文献[12-13]提出了概念相似度以及属性相似度的定义, 进而确定概念邻域, 实现了面对属性和对象概念格的压缩, 这些压缩方法是直接由形式背景出发, 实现了对概念格结构的高效压缩。
本文借鉴压缩理论, 探讨区间参数对概念格压缩度的影响规律, 构建基于压缩理论的区间参数优化模型。在对概念格进行压缩的过程中, 首先要从形式背景出发构建二元关系对, 计算二元关系对的相似度, 形成相似矩阵, 利用二元关系对的覆盖得到近邻空间;然后求解各参数下的每个对象的邻域, 从而实现对原始概念格的不同程度的压缩, 当压缩度趋于最大值时, 认为此时的区间参数值为最优。
1 预备知识 1.1 区间概念格概述定义1[14] 称(U, A, R)为一个形式背景, 其中:U={x1, x2, …, xn}为对象集, 每个xi(i≤n)称为一个对象;A={a1, a2, …, am}为属性集, 每个aj(j≤m)称为一个属性;R为U和A之间的二元关系, R⊆U⊗A。若(x, a)∈R, 则称x具有属性a。若(x, a)∉R则称x不具有属性a。
用1表示(x, a)∈R, 用0表示(x, a)∉R, 这样形式背景就可以表示为只含有0和1的表格。对于形式背景(U, A, R), 在对象集X⊆U和属性集B⊆A上分别定义运算:
| $ {{X}^{*}}=\{a|a\in A, \forall x\in X, (x, a)\in R\} $ |
| $ {{B}^{*}}=\{x|x\in U, \forall a\in B, (x, a)\in R\} $ |
其中:X*表示X中所有对象共同具有的属性集合, B*表示具有B中所有属性对象集合。
定义2[6] 对于形式背景(U, A, R), L(U, A, R)是其诱导的经典概念格[3], (M, N, Y)是粗糙概念[4]格(Rough Lattice, RL)上的粗糙概念。设有区间[α, β](0≤α < β≤1), 则α上界外延Mα:
| $ {{M}^{\alpha }}=\{x|x\in M, |f(x)\cap Y|/|Y|\ge \alpha, 0\le \alpha \le 1\} $ |
β下界外延Mβ:
| $ {{M}^{\beta }}=\{x|x\in M, |f(x)\cap Y|/|Y|\ge \beta, 0\le \alpha <\beta \le 1\} $ |
其中:Y是概念的内涵;|Y|是集合Y中包含元素个数;Mα表示可能被Y中至少α×|Y|个内涵属性覆盖的对象;Mβ表示可能被Y中至少β×|Y|个内涵属性所覆盖的对象。
定义3[6] 设形式背景(U, A, R), 三元序偶(Mα, Mβ, Y)称为区间概念, 其中:Y为内涵, 是概念的描述;Mα为α上界外延;Mβ为β下界外延。
定义4[6] 用Lαβ(U, A, R)表示形式背景(U, A, R)的全体[α, β]区间概念, 记:
| $ \left( {{M}^{\alpha }}_{1}, {{M}^{\beta }}_{1}, {{Y}_{1}} \right)\le \left( {{M}^{\alpha }}_{2}, {{M}^{\beta }}_{2}, {{Y}_{2}} \right)\Leftrightarrow {{Y}_{1}}\subseteq {{Y}_{2}} $ |
则“≤”是Lαβ(U, A, R)上的偏序关系。若Lαβ(U, A, R)中的所有概念满足“≤”偏序关系, 则称Lαβ(U, A, R)是形式背景(U, A, R)的区间概念格。
定义5[6] 设序偶(Mα, Mβ, Y)为区间概念格的任意节点, τβα(Y)=|Mβ|/|Mα|表示属性集Y在指定的参数α, β下所覆盖的对象关于指定关系R的近似精度;ρβα(Y)=1-τβα(Y)表示相应的粗糙度。
定理1 β不变时, τβα随α的减小而不增(0≤α < β≤1)。
定理2 不变时, τβα随β的增大而不增(0≤α < β≤1)。其中:|Mα|表示上界外延中元素个数;|Mβ|表示下界外延中元素个数。
1.2 压缩理论概述由形式背景出发, 构造对象与属性的二元关系对t=(x, a), 表示对象x具有属性a。
定义6[13] 设(U, A, R)为一形式背景, 设二元关系对t1=(x1, a1), t2=(x2, a2)(t1, t2∈R), 则t1与t2之间的相似度为:
| $ r({{t}_{1}}, {{t}_{2}})=\frac{1}{2}\left( \frac{\left| f({{x}_{1}})\bigcap f({{x}_{2}}) \right|}{\left| f({{x}_{1}})\bigcup f({{x}_{2}}) \right|}+\frac{\left| g({{a}_{1}})\bigcap g({{a}_{2}}) \right|}{\left| g({{a}_{1}})\bigcup g({{a}_{2}}) \right|} \right) $ |
其中算子f、g分别为:
| $ \begin{align} & \forall x\in U, f(x)=\{y|\forall y\in A, xRy\}; \\ & \forall y\in A, g(y)=\{x|\forall x\in U, xRy\}. \\ \end{align} $ |
令t1=(x1, a1), 则:
| $ [{{t}_{1}}]=\{{{t}_{2}}=({{x}_{2}}, {{a}_{2}})\in R\left| r({{t}_{1}}, {{t}_{2}}) \right.\ge \gamma \} $ |
其中:γ∈[0, 1];称[t1]为t1的γ相似类, 则{[t1]|t1∈R}构成了R集上的一个覆盖。
定义7[13] 设CR为R上的覆盖,
定义8[13] 设(R, CR)为覆盖近邻空间, ∀t∈R, 称∩{K|K∈CR}为t的邻居, 记为N(t)。同样的, 将对象x的邻居记作N(x)。
定义9[15] 设∀t(x, a)∈R的邻居为N(t), N(t)*表示含有属性a的二元关系对的邻居中所有对象的集合, 定义:
| $ N(t)_{\alpha }^{*}=\left\{ {{x}_{j}}\left| ({{x}_{j}}\in N{{(t)}^{*}})\wedge \frac{\left| {{x}_{j}}.Y\bigcap f(x) \right|}{\left| f(x) \right|}\ge \alpha ) \right. \right\} $ |
其中:α为区间概念格中的区间参数, |·|表示集合中包含元素个数, 即基数。N(t)α*表示N(t)中可能被f(x)(x具有的属性)至少覆盖α×|f(x)|个属性的对象集合。
定义10[15] 设∀x∈U, 则x的邻居N(x)=∩{N(tj)α*|tj=(x, aj)};N(x)′为N(x)中所有对象共同具有的属性构成的集合。
求解对象x的邻居N(x)的过程实际是聚类过程, 得到的是与x有一定相似程度的对象的集合。通过求解N(x)′可以删除对象x具有的一些属性, 这些被删除的属性具有较弱的关联性, 因此含有这些属性的关联规则的置信度较低。
定义11[15] 设(U, A, R)为形式背景, 则定义算子如下: N(x)′为对象x的邻居共同具有的属性;α和β为区间概念格中的区间参数。
| $ \begin{gathered} Y' = Y \hfill \\ \left\{ \begin{gathered} {M^{\alpha '}} = \left\{ {x\left| {x \in {M^\alpha } \wedge \frac{{\left| {N(x)' \cap Y} \right|}}{{\left| Y \right|}} \geqslant \alpha } \right.} \right\} \hfill \\ {M^{\beta '}} = \left\{ {x\left| {x \in {M^\beta } \wedge \frac{{\left| {N(x)' \cap Y} \right|}}{{\left| Y \right|}} \geqslant \beta } \right.} \right\} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $ |
对于∀(Mα, Mβ, Y), 若有Mα′=Mα且Mβ′=Mβ, 则称(Mα, Mβ, Y)为压缩后的区间概念。对区间概念格中的任一概念(Mα, Mβ, Y)按照上式中的算子进行计算, 如果满足相等的条件, 则保留下来;否则删除。最后得到的概念格为压缩概念格记为Lαβ′(U, A, R)。
定义12[15] 设(U, A, R)为形式背景, Lαβ(U, A, R)表示形式背景(U, A, R)的全体[α, β]区间概念, Lαβ′(U, A, R)表示经过压缩得到的全体区间概念, 定义:Rd=(|Lαβ(U, A, R)|-|Lαβ′(U, A, R)|)/|Lαβ(U, A, R)|为压缩度。其中|Lαβ(U, A, R)|、|Lαβ′(U, A, R)|分别表示压缩前与压缩后的概念数量。
定理3[15] 设(U, A, R)为形式背景, 则Lαβ′(U, A, R)⊆Lαβ(U, A, R), 即压缩后的概念集是压缩前概念集的子集。
区间参数α影响着二元关系对邻域N(t)α*的取值, 即同一属性的二元关系对的邻居中所有对象的集合中具有属性数量的比例超过α的对象的集合。在区间参数[α, β]下求解对象的邻域N(x)以及邻域中所有对象的共同具有的属性构成的集合N′(x), 区间概念上下界外延定义中的f(x)用N(x)′来代替, 得到的Mα′与Mβ′使得格结构中的重要特征保留下来, 随着α和β取值的不同, 在形式背景中被舍掉的关系也会不同。
1.3 定参数下概念格压缩算法算法1 Lα0β0(U, A, R)压缩算法。
输入 形式背景M, 区间参数[α0, β0], 相似类阈值γ0∈[0, 1];
输出 概念格压缩度Rd。
步骤1 由形式背景M提取出二元关系对集合R={t1, t2, …, tn}, 并根据定义6计算相似度, 得到二元关系对相似度矩阵。
步骤2 设定γ0∈[0, 1], 根据定义6求得t1, t2, …, tn的γ0相似类, 进而得到由相似类构成的覆盖CR, 由定义8得到t1, t2, …, tn的邻居;根据定义9以及给定区间参数[α0, β0]分别计算每一个ti对应的N(t)*与N(t)α*。
步骤3 对步骤2得到的N(t)α*, 根据定义10计算得到每一个对象的邻居N(x)及共同具有的属性N(x)′。
步骤4 由给定的形式背景M得到区间概念集[7], 记录概念数n0;然后对集合中的每一个概念用定义11中的算子及判定方法进行区间概念格的压缩, 记录压缩后的概念格中概念数n1;最后计算概念格的压缩度Rd=(n0-n1)/n0并输出。
步骤5 算法结束。
该算法是直接从形式背景出发进行的压缩。通过计算N(x)′保留了形式背景中的重要属性, 提高了关联规则的可信度。将N(x)′与区间概念的上下界外延联系得到压缩算子, 由此实现区间概念格的压缩。同时可以调整相似度阈值γ, 控制对象邻域的大小, 达到动态压缩的效果。
2 基于压缩度的区间参数优化模型为了获得最优的区间参数, 引入压缩度算子来衡量区间参数的优劣, 第1章已经给出定参数下概念格压缩算法, 本章通过改变区间参数获得各参数下的概念格压缩度, 根据压缩度的大小和趋势来确定最优参数的取值。由于压缩度只与概念格中概念的数目有关, 因此变参数后无需每次构建格结构, 只需要更新概念获得更新后的概念集合。
2.1 基于参数变化的概念集合的更新当区间参数α和β发生变化时, 概念格中的概念会相应变化。根据概念变化的特征, 给出如下几类概念的定义:
定义13 设区间概念格Lα0β0(U, A, R), 当区间参数由[α0, β0]变为[α1, β1]时, 若∃G1=(Mα1, Mβ1, Y)∈Lα1β1(U, A, R), 且G1=(Mα1, Mβ1, Y)=(Mα0, Mβ0, Y)=G0∈Lα0β0(U, A, R), 则称G0为不变概念(保留)。
定义14 设区间概念格Lα0β0(U, A, R), 当区间参数由[α0, β0]变为[α1, β1]时, 若∃G1=(Mα1, Mβ1, Y)∈Lα1β1(U, A, R), 使得Mα1=∅, 称G1=(Mα1, Mβ1, Y)为空概念(删除)。
定义15 设更新后区间概念格中的概念G′, 且MG′.fatherα=MG′.childrenα, MG′.fatherβ=MG′.childrenβ, YG′.children⊆YG′.father, 则称G′children为冗余概念(删除)。
定义16 设区间概念格Lα0β0(U, A, R), 当区间参数由[α0, β0]变为[α1, β1]时, 若∃G1=(Mα1, Mβ1, Y)∈Lα1β1(U, A, R), Mα1⊆Mα0, Mβ1⊆Mβ0, (Mα0, Mβ0, Y)=G0∈Lα0β0(U, A, R), 则称β0=1为G0的扩展概念。
定义17 设区间概念格Lα0β0(U, A, R), 当区间参数由[α0, β0]变为[α1, β1]时, 若∃G1=(Mα1, Mβ1, Y)∈Lα1β1(U, A, R), Lα1β1(U, A, R), Mα1⊆Mα0, Mβ1⊆Mβ0, (Mα0, Mβ0, Y)=G0∈Lα0β0(U, A, R)则称G1为G0的缩减概念。
为了减小概念更新的工作量, 这里要求区间参数等步长增减变化。设定形式背景中条件属性A的个数为n, 参数α由1/n等步长变化到n/n, 相应的参数β由n/n等步长变化到1/n, 同时保持α≤β。区间参数变化取值见表 1。
| 表 1 区间参数取值表 |
下面给出固定参数β, 等步长增加α的概念集合更新算法。
算法2 基于参数变化的区间概念集合更新算法。
输入 形式背景M, 参数β=1;
输出 更新后的概念集合。
步骤1 根据形式背景中条件属性的个数n确定参数α的初始值为α0=1/n, 构建[1/n, 1]下的概念集合CS1, 由定义15删除概念集合中冗余的子概念, 得到概念集合CS1′。
步骤2 令α1=α0+1/n, 若概念集合CS1中概念C的内涵个数|Y|=1, 则概念C为不变概念, 保留;若[|Y|×α1]>[|Y|×α0](表示不超过|Y|×α1的最大整数), 转步骤3。
步骤3 根据定义17对概念上界外延进行缩减, 若缩减后的上界外延为空集, 则删除概念C;否则得到更新后的概念C′。
步骤4 根据定义15删除更新后的概念集合CS2中的冗余概念, 得到新集合CS2′;转步骤2继续更新概念集合CS2。
步骤5 输出更新后的概念集合CS1′, CS2′, CS3′, …。
步骤6 算法结束。
该算法根据概念中的内涵基数就可以直接判断该概念是否需要更新, 无需遍历原始概念集合中的每个概念, 大幅降低了重构概念的工作量。需要更新的概念再进行相应的缩减和删除操作, 最终去冗余得到新的概念集合。同理, 改变参数β的取值, 由1等步长减小到1/n(α≤β), 每改变一次就按照算法2进行一次输出, 得到所有可能区间参数下的概念集合, 从而进行压缩并计算不同区间参数下的压缩度。
2.2 基于压缩度的区间参数优化模型先前对区间参数的优化考虑到的因素包括格结构的更新度、概念节点数目以及提取的关联规则数目和精度, 试图找到当格结构趋于稳定(即更新度趋于0), 概念节点数适中以及提取的关联规则数目较多且精度较高时的区间参数值。这些分析忽略了形式背景中较弱的关联关系会导致概念冗余, 对概念格进行压缩能够在一定程度上解决这些问题。本节提出的基于压缩度的区间参数优化模型, 就是根据压缩度大小来衡量区间参数取值的优劣, 以找到最优值。
算法3 基于压缩度的区间参数优化模型。
输入 形式背景M, 相似类阈值γ∈[0, 1];
输出 合适的区间参数以及所对应的压缩度。
步骤1 从形式背景获得属性个数n, 设置步长λ=1/n, 初始区间参数α0=1/n, β0=1, 构建概念集合CS0′, 按照算法1得到压缩度Rd1。
步骤2 令α1=α0+1/n, β0=1, 按照算法2更新概念集合CS0得到CS1′。
步骤3 按照算法1得到压缩度Rd2, 若Rd2≤Rd1, 转步骤2;若Rd2>Rd1, 输出区间参数α和β以及Rd2。
步骤4 继续令α1=α0+1/n, β0=1-1/n, 按照算法2更新概念集合, 转步骤3。
步骤5 继续令α1=α0+1/n, β0=1-2/n且α≤β, 直至找到最大的压缩度并输出。
步骤6 算法结束。
2.3 模型分析为了找到最优区间参数[α, β], 首先明确参数所有的取值, 模型中固定参数β的取值等步长改变α可以得到n组参数对, 根据压缩度的大小能够求解出最优的参数α;参数β等步长减小1/n, 再改变α的取值同时保证α≤β可以得到n-1组参数对, 依此类推获取所有参数对的可能取值, 根据压缩度之间大小对比求解出最优区间参数[α, β], 显然随着形式背景中条件属性的增加, 参数对可能的取值会增多, 在后续更新以及计算压缩度上效率会降低。但是由于在设计更新算法时, 参数按照等步长增减, 原始概念集合中会有相当一部分概念为不变概念直接保留下来, 这样每次概念集合的更新工作并不是难以完成, 进而获取所有可能参数对下的压缩度, 对比大小和趋势, 总结得出最优的区间参数。
3 实例分析为了简便起见, 本文固定参数β=1, 只探讨参数α的改变对区间概念格压缩度的影响规律。下面给出属性集A={a, b, c, d, e}、对象集U={1, 2, 3, 4, 5, 6, 7, 8}的形式背景见表 2。
| 表 2 形式背景 |
根据表 2给定的形式背景按照基于压缩度的区间参数优化模型寻找最优区间参数。
1)计算R中二元关系对之间的相似度。由形式背景得到二元关系对:t1=(1, c), t2=(1, d), t3=(2, b), t4=(2, d), t5=(2, e), t6=(3, a), t7=(3, e), t8=(4, a), t9=(4, b), t10=(5, d), t11=(5, e), t12=(6, b), t13=(6, c), t14=(6, d), t15=(7, a), t16=(8, b), 得到二元关系对集合R={t1, t2, …, t16}。对R中的任意两个二元关系对ti、tj, 利用定义6计算它们之间的相似度, 部分结果见表 3。
| 表 3 相似度矩阵 |
2)设定初始区间参数[1/5, 1]和相似度阈值γ=0.55∈[0, 1], 由相似度矩阵得到每个二元关系对的γ相似类, 进一步得到覆盖CR。根据CR计算所有邻居N(t), 对应的N(t)*及N(t)1/5*。二元关系对所有的邻居见表 4。
| 表 4 二元关系对邻居N(t) |
二元关系对的邻居中所有对象的集合N(t)*, 部分结果:N(t1)*={1, 6}, N(t2)*={1, 2, 5, 6}, N(t3)*={2, 4, 6, 8}, N(t4)*={1, 2, 5, 6}, …, N(t14)*={1, 2, 5, 6}, N(t15)*={3, 4, 7}, N(t16)*={2, 4, 6, 8}。二元关系对的邻居中被f(x)(x具有的属性)至少覆盖1/5×|f(x)|个属性的对象集合N(t)1/5*, 部分结果:N(t1)1/5*={1, 6}, N(t2)1/5*={1, 2, 5, 6}, N(t3)1/5*={2, 4, 6, 8}, N(t4)1/5*={1, 2, 5, 6}, …, N(t14)1/5*={1, 2, 5, 6}, N(t15)1/5*={3, 4, 7}, N(t16)1/5*={2, 4, 6, 8}。
3)根据定义10计算每一个对象的邻居N(x)以及相应的N(x)′, 例如:N(1)=∩N1/5*(t1)∩N1/5*(t2)={1, 6}, N(2)=∩N1/5*(t3)∩N1/5*(t4)∩N1/5*(t5)={2}, N(3)=∩N1/5*(t6)∩N1/5*(t7)={3}。结果见表 5。
| 表 5 [1/5, 1]下对象邻居N(x)和共有属性N(x)′ |
4)构建原始区间[1/5, 1]概念集合CS1, 见表 6。
| 表 6 [1/5, 1]概念集合 |
根据定义11中的算子及判定方法进行区间[1/5, 1]概念格的压缩, 例如:概念C3=({1, 6}, {1, 6}, {c}), 其内涵Y=c, 上界外延为{1, 6}, 下界外延为{1, 6};因为N(1)′={c, d}, N(6)′={b, c, d}, 所以(|N(1)′∩Y|)/|Y|=(|cd∩c|)/|c|=1, (|N(6)′∩Y|)/|Y|=(|bcd∩c|)/|c|=1, 又因为α=1/5, β=1, 1/5 < 1≤1, 因此概念C3=({1, 6}, {1, 6}, {c})是压缩后区间[1/5, 1]概念格中的概念。压缩后的概念集合为{C1, C2, C3, C4, C5, C7, C8, C9, C10, C11, C12, C15, C16}, 计算压缩度Rd=(20-13)/20=0.35。
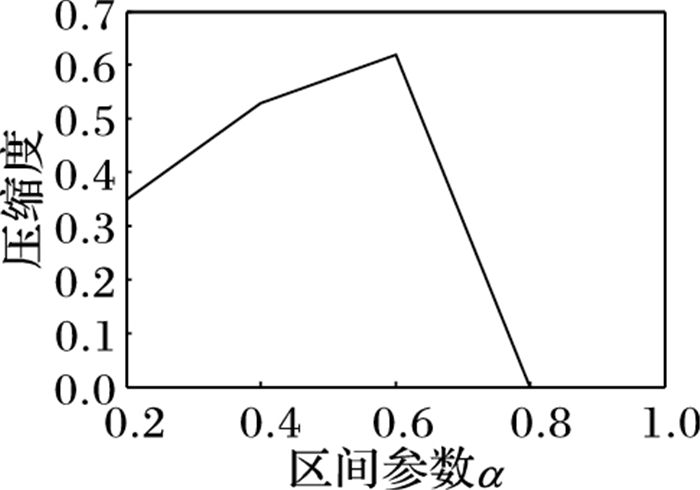
5)根据模型中的算法继续计算区间参数[2/5, 1], [3/5, 1], [4/5, 1]以及[1, 1]的压缩度。绘制趋势如图 1。
|
图 1 α与区间概念格压缩度关系 |
由图 1可以看出当区间参数α=3/5, β=1时, 区间概念格的压缩度达到最大值为0.62, 即在该区间参数下进行了最大程度的压缩, 使得冗余达到最小, 去除了关联性较弱的关系, 保留了关联性最强的关系, 从而构建较为简洁的格结构, 挖掘置信度较强的关联规则。文献[8]中的区间参数优化模型得到的结论是:当参数α=0.5, β=1时, 概念节点数较多, 关联规则数最多以及关联规则的平均置信度水平较高, 与此同时概念格的更新度达到最低值, 表明格结构趋于稳定。如此看来基于压缩度的区间参数优化模型得到的最优区间参数值与文献[8]中的结论大致相同, 进一步印证了该模型的可靠性和有效性。鉴于篇幅的原因, 文中的实例数据量并不是很大, 为了更有力地说明该模型的准确性, 建议增加形式背景中的条件属性以及对象的个数, 按照模型中的算法进行模拟, 得出的结果可信度更高。
4 结语本文主要基于压缩理论角度对区间参数的取值问题展开分析, 根据形式背景构建二元关系对, 计算二元关系对的相似度, 形成相似矩阵, 利用二元关系对的覆盖得到近邻空间, 然后求解各参数下的每个对象的邻域, 从而实现对原始概念格的不同程度的压缩, 当压缩度趋于最大值时, 认为此时的区间参数值为最优。通过分析, 给出了基于参数变化的概念集合更新算法以及基于压缩理论的区间参数优化模型, 经实例验证得到区间参数α与压缩度大致趋势, 初步确定参数α取得靠近中间值时使得压缩度最大、冗余最少以及提取的关联规则置信度较强。该模型对区间概念格的参数选取提供了又一种切实有效的方法。
| [1] | HAN J W, KAMBER M. Data Mining:Concepts and Techniques[M]. Beijing: China Machine Press, 2006 : 157 -179. |
| [2] | GODIN R, MISSAOUI R, ALAOUI H. Incremental concept formation algorithm based on Galois (concept) lattices[J]. Computational Intelligence, 1995, 11 (2) : 246-267. doi: 10.1111/coin.1995.11.issue-2 |
| [3] | GODIN R, MINEAU G W, MISSAOUI R. Incremental structuring of knowledge bases[C]//Proceedings of the 1995 International Symposium on Kownledge Retrieval, Use, and Storage for Efficiency. California:University of California, 1995:179-193. |
| [4] | YANG H F, ZHANG J F. A new concept lattice structure:rough concept lattice[C]//Proceedings of the 17th Meeting of Computer Science and Technology Application. Hefei:University of Science and Technology of China Press, 2006:212-216. |
| [5] | YAO Y Y, CHEN Y H. Rough set approximations in formal concept analysis[C]//Proceedings of the 2004 Annual Meeting of the North American Fuzzy Information Processing Society. Berlin:Springer-Verlag, 2004:73-78. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1336252 |
| [6] | 刘保相, 张春英. 一种新的概念格结构--区间概念格[J]. 计算机科学, 2012, 39 (8) : 273-277. ( LIU B X, ZHANG C Y. A new concept lattice structure:interval concept lattice[J]. Computer Science, 2012, 39 (8) : 273-277. ) |
| [7] | ZHANG C Y, WANG L Y, LIU B X. An effective interval concept lattice construction algorithm[J]. ICIC Express Letters, Part B:Applications, 2014, 5 : 1573-1578. |
| [8] | LI M X, ZHANG C Y, WANG L Y, et al. Parameters optimization and interval concept lattice update with change of parameters[J]. ICIC Express Letters, 2016, 10 (2) : 339-346. |
| [9] | 王立亚, 张春英, 刘保相.基于区间概念格的三支决策动态策略调控模型[J/OL].计算机工程, [2016-01-20].http://www.cnki.net/kcms/detail/11.2127.TP.20151231.1349.038.html. ( WANG L Y, ZHANG C Y, LIU B X. Dynamic strategy regulation model of three-way decisions based on interval concept lattice and its application[J/OL].Computer Engineering, [2016-01-20].http://www.cnki.net/kcms/detail/11.2127.TP.20151231.1349.038.html. ) |
| [10] | ZHANG W X, WEI L, QI J J. Attribute reduction in concept lattice based on discernibility matrix[C]//Proceedings of the 10th International Conference on Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing. Berlin:Springer-Verlag, 2005:157-165. |
| [11] | 李仲玲, 米据生. 形式背景的交约简[J]. 计算机科学与探索, 2010, 4 (12) : 1148-1152. ( LI Z L, MI J S. Meet-reduction in formal context[J]. Journal of Frontiers of Computer Science and Technology, 2010, 4 (12) : 1148-1152. ) |
| [12] | 魏玲, 李强. 面向属性概念格基于覆盖的压缩[J]. 电子科技大学学报, 2012, 41 (2) : 299-304. ( WEI L, LI Q. Covering-based reduction of property-oriented concept lattices[J]. Journal of University of Electronic Science and Technology of China, 2012, 41 (2) : 299-304. ) |
| [13] | 陈永平, 杨思春. 面向对象概念格的压缩[J]. 计算机工程与应用, 2013, 49 (19) : 119-122. ( CHEN Y P, YANG S C. Reduction of object-oriented concept lattices[J]. Computer Engineering and Applications, 2013, 49 (19) : 119-122. ) |
| [14] | 张文修, 仇国芳. 基于粗糙集的不确定决策[M]. 北京: 清华大学出版社, 2006 : 185 . ( ZHANG W X, QIU G F. Uncertain Decision based on Rough Set[M]. Beijing: Tsinghua University Press, 2006 : 185 . ) |
| [15] | 张春英, 王立亚, 刘保相. 基于覆盖的区间概念格动态压缩原理与实现[J]. 山东大学学报(理学版), 2014, 49 (8) : 15-21. ( ZHANG C Y, WANG L Y, LIU B X. Dynamic reduction theory for interval concept lattice based on covering and its realization[J]. Journal of Shandong University (Natural Science), 2014, 49 (8) : 15-21. ) |




