实测地层剖面是区域地质调查工作中的重要环节,是研究一个地区基本地质情况、确定地层的岩石组成、岩相、接触关系以及古生物赋存情况的基础性工作。早在20世纪70年代开始,大量学者充分讨论了实测剖面中地层厚度的计算方法(肖水清,1977;佟再三,1983;庄培德,1983;许明七,1985;黄立华,1986;沈忠悦,1988;漆树基,1991;许边远,1998;郭福生等,1999;杨光忠,2002),建立了通用的地层厚度计算公式。传统的剖面计算和绘制工作繁复,随着计算机技术的迅速发展,现在不少学者开始深入研究实测地层剖面绘制的计算机实现方法(李义才,2001;方世明等,2002;刘杰等,2009;王铸,2009;裴丽娜,2011;杨利容等,2011;陈志军等,2012),以节省人力和时间。当前实测地层剖面绘制有直线和导线两种方法。直线法要求所有地层产状基本一致,野外测量时,导线前进方向始终与地层走向垂直,导线前进方向即为总导线方向,在绘制过程中只需要按照测量数据逐段绘制,但这种方法应用的前提条件颇为苛刻,常难以满足。第二种方法为导线法,要求导线前进方向可在地层倾向±30°以内摆动,采用二次二维投影法绘制实测剖面图,但这种方法也存在许多不足之处,本文针对这些问题进行详细的讨论,进而提出消除这些缺陷的一种新方法——三维投影法,并以实例来验证该方法的优势。
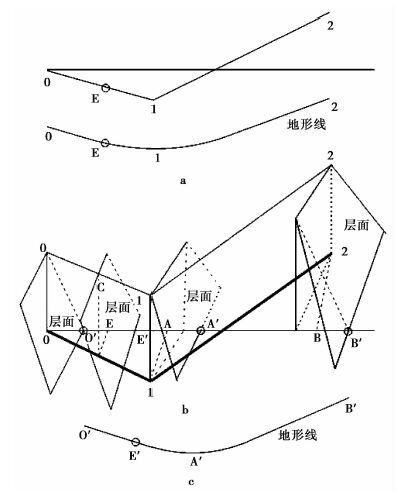
1 导线法绘制的原理缺陷 1.1 常规导线段的缺陷图 1a是0—1—2导线的导线平面图和实测剖面地形线,图 1b为0—1—2导线的三维空间分布示意图。按照导线法的绘制方法,图 1a中的导线平面图是 图 1b中0—1—2细实线的平面投影,即 图 1b的0—1—2粗实线。 图 1a中的实测剖面地形线的导线转折点横坐标为导线平面图在总导线方位上的垂直投影,其横坐标为 图 1b所示的0、A、B 3点,由 图 1b可以看出,实际转折点并不是0、A、B点,而是0′、A′、B′点。同理,0—1导线上的边界点C,按导线法其横坐标是 图 1b的E点,而实际边界点是E′点,因此地形线的实际位置应如 图 1c所示。由此可见,常规导线段确定的导线转折点和地层边界点并非真实地层边界点位置,这个问题是在第二次向总导线方位进行垂直投影时产生的。
|
图1 导线法对常规导线段影响示意图 Fig.1 The influence of the leading line method on the regular leading line |
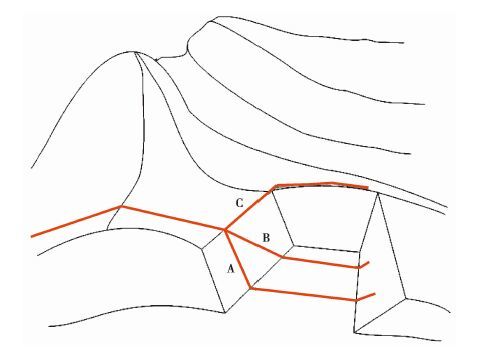
图 2为层面陡坎处理的路线图。路线C是沿地层走向拉测绳平移,然后沿地层倾向进行测量;路线B是沿层面斜拉测绳到层面底部,然后沿地层倾向进行测量;路线A是沿地层倾向拉测绳到层面底部,然后沿地层倾向进行测量。路线C被认为是沿层面平移,而对路线A与路线B在实测地层剖面中按导线法确定的地形线性质存在不同看法:1)认为地形线为岩性线,2)认为地形线为平移线。
|
图2 实测地层剖面层面陡坎处理路线图 Fig.2 The different lines on the stratum scarp in the measured geological section |
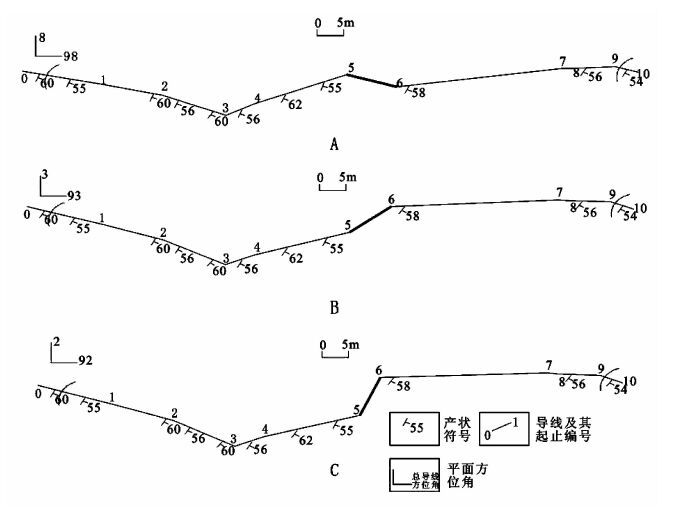
为了讨论导线法对不同测量路线的影响,按照导线法绘制路线A、B、C的导线平面图(图 3),其中粗实线5—6导为 图 2中A、B、C所示的导线。
|
图3 3种不同测量方式的导线平面图 Fig.3 The plane graph of the three different leading lines |
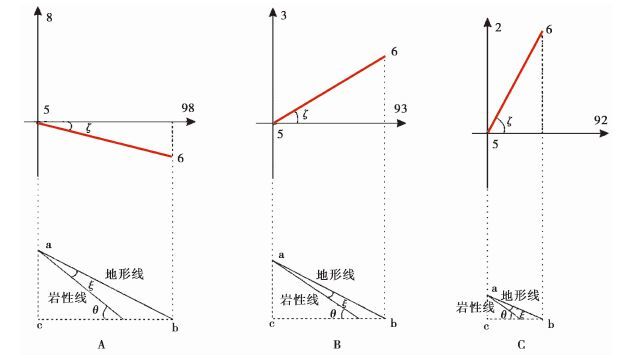
从 图 3可知,在不同路线测量方式中,5—6导的变化导致了总导线方位角的变化。把3种不同测量方式中5—6导的导线平面图和地形线进行绘制(图 4),ab是地形线,要确定它是平移线还是岩性线,关键在于确定∠abc与视倾角θ的大小关系:若ab地形线是岩性线,则∠abc等于视倾角θ;若ab地形线是平移线,则∠abc不等于视倾角θ, 即从a点绘制的岩性线与ab之间存在夹角ξ。
|
图4 3种不同测量方式的平移导线所对应的地形线 Fig.4 The rolling topography of the translational line with different measured line |
如 图 4所示,对于A、B、C 3种情况,∠abc由下式可得:
\[\text{tan}\angle \text{abc}=\text{ac/bc}\]
(1)
| \[\text{ac=}l\sin \beta \] | (2) |
bc段是由5—6导的水平距垂直投影到总导线方位上得到的,由 图 4可知:
\[\text{bc}=l\cos \beta \cos \zeta \]
(3)
把公式(2)和公式(3)式代入公式(1)得到:
| \[\text{tan}\angle \text{abc}=\frac{l\sin \beta }{l\cos \beta \cos \zeta }=\frac{\sin \beta }{\cos \beta \cos \zeta }\] | (4) |
其中A种情况由于沿地层倾向测量,因此真倾角等于坡角,用α表示真倾角,由公式(4)可得:
| \[\text{tan}\angle \text{abc}=\frac{\sin \beta }{\cos \beta \cos \zeta }=\frac{\sin \alpha }{\cos \alpha \cos \zeta }\] | (5) |
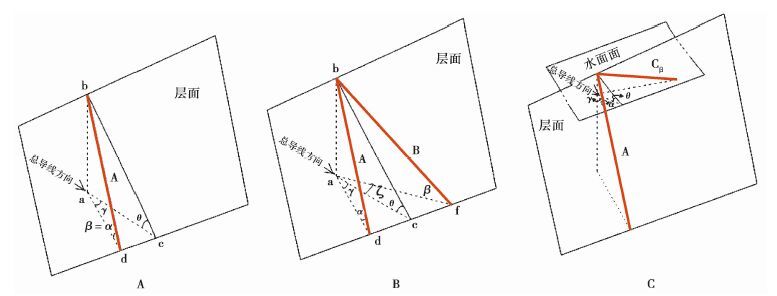
图 5为A、B、C的3种情况下视倾角计算示意图。
|
图5 3种情况下的视倾角计算示意图 Fig.5 The sketch map of the calculation of apparent inclination under the three different leading lines |
如 图 5所示θ角为视倾角,α角为真倾角,β角为坡角,γ角为地层倾向与总导线方位的夹角。A、B、C的3种情况下,真倾角与视倾角的关系如下式:
| \[\tan \theta =\frac{\text{ab}}{\text{ac}}=\frac{\text{bd}\sin \alpha }{\text{bd}\cos \alpha /\cos \gamma }=\tan \alpha \cos \gamma \] | (6) |
A路线情况时,即沿导线倾向方向测量层面时,若地形线为岩性线时,则∠abc等于视倾角,由公式(5)和公式(6)得:
| \[\cos \zeta \cos \gamma =1\] | (7) |
因导线方位与地层倾向一致,所以导线方位与总导线方位之间的夹角ζ等于地层倾向与总导线方位之间的夹角γ,令φ角表示总导线方位角,η表示5—6导线方位角,由公式(7)式可得:
| \[\cos {{\left( \varphi -\eta \right)}^{2}}=1\] | (8) |
由公式(8)可知
| \[\varphi =\eta \] | (9) |
公式(9)说明只有在计算的总导线方位角恰好与层面陡坎上5—6分导线方位角一致,即总导线方位角与地层倾向方位角一致时,图 4绘制的地形线ab才是岩性线,这对野外工作而言是非常苛刻的条件,难以达到。因此在沿层面陡坎的倾向进行测量时,图 4中的地形线ab应为平移线而非岩性线。只有在总导线方位角与层面陡坎上的分导线方位角相等时,才会出现平移线与岩性线恰好重合的现象。
在层面陡坎上斜拉测绳时,即B路线测量方式,若地形线为岩性线,则∠abc等于视倾角,由公式(4)和公式(6)得到:
| \[\frac{\tan \beta }{\cos \zeta }=\tan \alpha \cos \gamma \] | (10) |
如 图 5b所示,真倾角α、坡角β、5—6导线与总导线方位角的夹角ζ,以及地层倾向与总导线方位角的夹角γ的关系可以表示为:
| \[\tan \beta =\frac{\text{ab}}{\text{af}}=\frac{\text{bd}\sin \alpha }{\text{bd}\cos \alpha /\cos \left( \zeta +\gamma \right)}=\tan \alpha \cos \left( \zeta +\gamma \right)\] | (11) |
将公式(11)代入公式(10)可得:
| \[\cos \left( \zeta +\gamma \right)=\cos \zeta \cos \gamma \] | (12) |
即得:
| \[\sin \zeta \sin \gamma =0\] | (13) |
可以看出当ζ为零或γ为零时,公式(13)成立,表明当导线总方位角与地层倾向恰好一致时,或当导线总方位角与5—6导线方位角恰好一致时,图 4中的ab地形线为岩性线,这对野外工作而言均为苛刻条件,难以达到。因此沿层面陡坎斜拉导线时,图 4中的地形线ab为平移线而非岩性线,只有在计算得到的总方位角与地层倾向方位角一致时或当导线总方位角与层面陡坎上的导线方位角一致时,才会出现平移线与岩性线恰好重合的现象。近平行于地层走向的C路线,与B路线在原理上相同,公式也相同,只是投影水平面不同,据此可以得到与B路线相同的地形线认识结论。
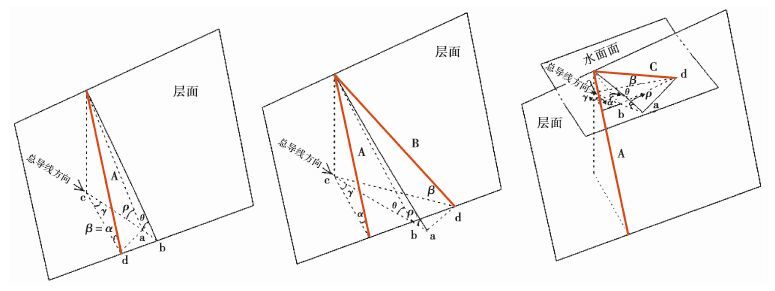
造成层面陡坎上地形线为平移线以及地形线与岩性线存在夹角的原因(图 6),是导线法的绘制方式。
|
图6 层面陡坎处理的平移线与层面线夹角实质图 Fig.6 The substance for the angle between the stratum line and the translational line on the stratum scarp |
如 图 6所示,在导线法绘制实测地层剖面时,地形线是依靠二次二维投影形成的,一次是导线斜距在平面上投影,形成cd段,然后水平距向总导线方向垂直投影形成ca段,因此形成ρ角,即为 图 4中的∠abc。而视倾角则为 图 6中的θ角,此θ角是在三维空间中计算获得,由此形成了θ和ρ角的差异性,形成了地形线与岩性线之间的夹角。只有在计算的总导线方位角与层面陡坎的倾向方位角一致时或与层面陡坎分导线方位角一致时,θ和ρ才会一致。因此地形线与岩性线之间的夹角是由采用二维空间二次投影得到地形线和采用三维空间计算得到的视倾角之间的矛盾造成的。
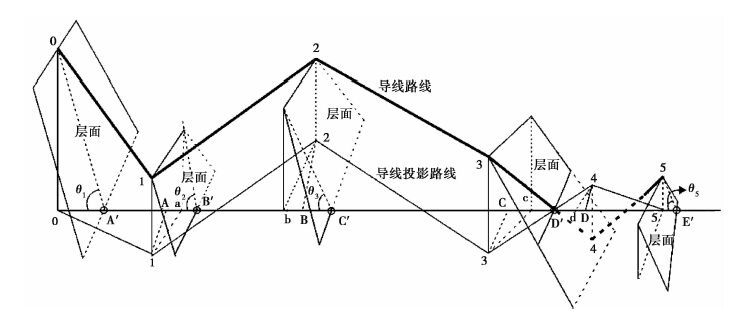
2 实测剖面绘制新方法——三维投影法由 图 3可以看出,当选择不同的测量路线时,会得到不同的导线平面图和不同形态的实测地层剖面图。在实测地层剖面平移段的处理中,也常采用不同的方式:1)不在实测地层剖面图中绘制平移段,而只标注;2)按实际测量长度绘制平移段;3)为了图形美观只按固定长度绘制平移段,因此同一实测地层剖面,形成了不同形态的导线平面图和地层剖面图,这不利于资料识读。实测剖面的绘制,实质上是每一导测量结果在总导线方位上的投影。我们提出一种三维投影绘制方法,能够消除导线法的原理缺陷,并且使平移段在导线平面图中仍然正确显现,而在地层剖面图中不再显示,使地层剖面图便于解读和符合实际,其原理如 图 7所示。
|
图7 实测地层剖面三维投影法原理 Fig.7 The theory of the profile drawing with 3D projection of measured geological section |
在 图 7中,粗线0—1—2—3—4—5是野外实测导线路线图,其中3—4导在层面陡坎上。细线0—1—2—3—4—5是导线平面图,即导线在水平面上投影图。按照导线法绘图方法,导线平面图在总导线上的投影是地形线转折点的水平坐标,即图中的0、A、B、C、D和5。这6个点实际上并不是实测地层在总导线方位上的真实边界点,实测层面在总导线方位线上的边界点应为A′、B′、C′、D′、E′的5点。因此只要确定了这5点的水平坐标,就确定了地形线转折点的水平坐标,地形线转折点纵坐标仍为地形高差。要想确定5点的水平坐标,我们首先在导线平面图上从1、2、3、4点做地层走向的平行线,交总导线方位线于a、b、c、d。这样我们就得到了0、a、b、c、d、5。通过这6个点就可以确定A′、B′、C′、D′和E′的5点。从图中不难看出A′、B′、C′、D′和E′分别是0、a、b、c和5沿总导线方向前移一段距离得到,而这些距离0—A′,a—B′,b—C′,c—D′和5—E′分别与0、a、b、c和5点高差的比值构成5个地层视倾角的余切。
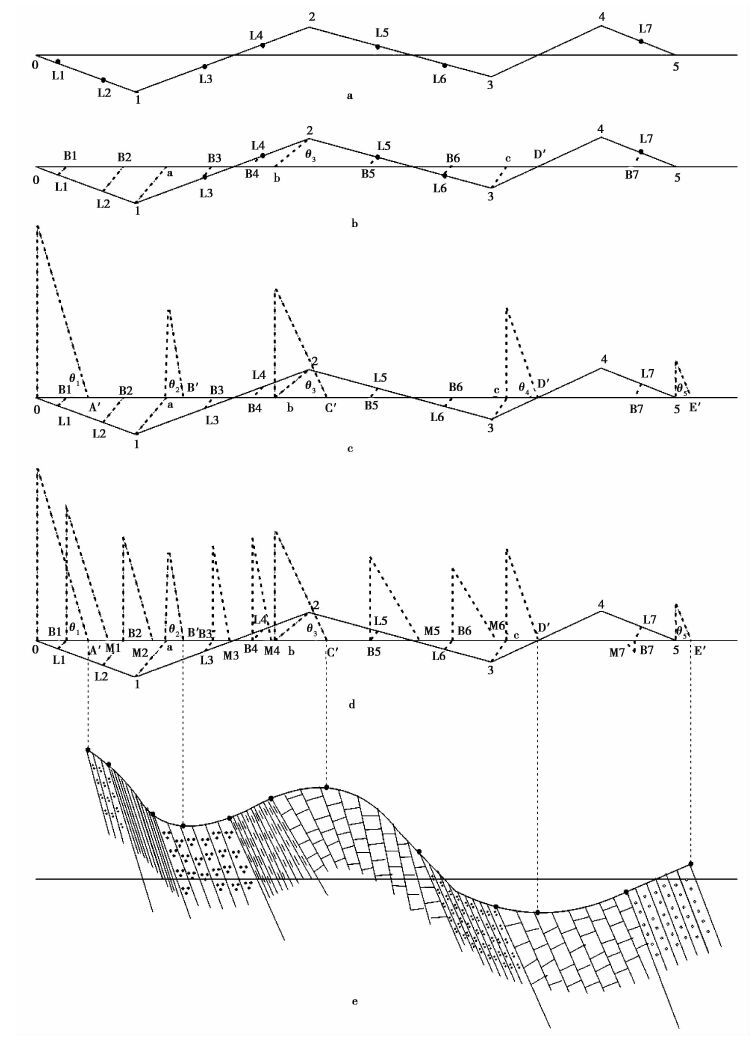
如 图 8a所示,首先把 图 7所示的各导线投影到水平面上,得到导线平面图,其中3—4为平移导线,并把系界线点、组界线点、地层界线点投影到导线平面图上,即图中L1~L7点。如 图 8b所示,以导线平面图各转折点、系界线点、组界线点、地层界线点为端点,做平行于地层走向方向的直线,与总导线方位线分别交于a、b、c和B1~B7等点。如 图 8c所示,以1、a、b、c和5为垂足,按相对高差做垂线,然后以视倾角θ1,θ2,θ3,θ4,θ5大小按 图 8c做图,交总导线方位线于A′、B′、C′、D′和E′点,这5点所对应的水平坐标即为总导线方位线上的地形线转折点的水平坐标。如 图 8d所示,以B1~B7为垂足按 图 8c方式以相对高差做垂线,再以相应视倾角大小做直线,交总导线方位线于M1~M7点,需要注意的是当相对高差为负值时,按视倾角大小做直线时,应与相对高差为正值时方向相反(如 图 8d中B7点所示)。如 图 8e所示,以A′~E′点垂向投影,投影的垂向大小按相对高差衡量,以投影后的5点圆滑绘制直线,即为地形线,再把M1~M7点垂向投影到地形线上,按界线性质绘制地层界线长度,然后绘制岩性线并填充岩性花纹,得到最终的实测地层剖面。为了详细清晰地阐述绘制步骤,我们把每一步分图幅绘制,在实际制图时,图 8a~ 图 8d等4幅图可以绘制在同一幅图上。
|
图8 实测剖面三维投影绘图法步骤 Fig.8 The steps of the profile drawing with 3D projection of the measured geological section |
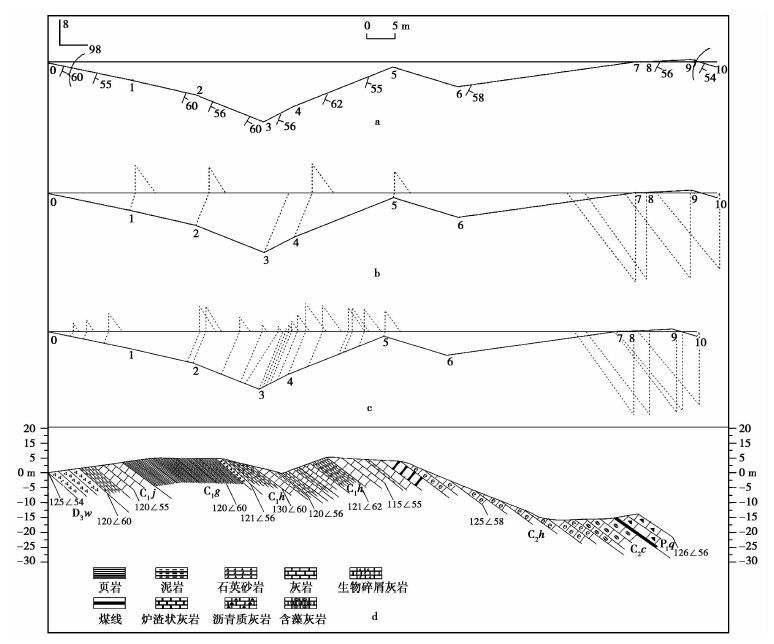
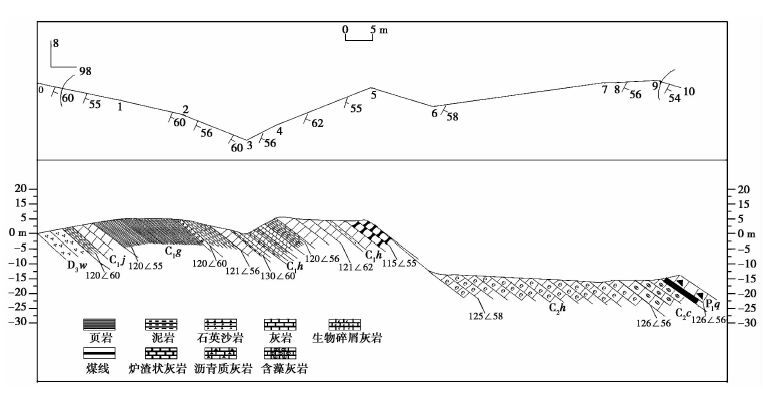
为了进一步验证三维投影法的实用性,选取安徽巢湖市麒麟山背斜东南翼石炭纪地层的实测数据,进行了三维投影法的绘制。实测数据在和州组顶面上是沿地层倾向方向测量的。三维投影法绘制结果如 图 9所示,导线法绘制结果如 图 10所示。
|
图9 安徽巢湖市凤凰山地区麒麟山背斜东南翼石炭纪地层三维投影法实测地层剖面图 a. 导线平面图;b. 三维投影法确定地形转折点位置图;c. 三维投影法确定地层界线点位置图;d. 用b和c投影绘制的实测地层剖面图 Fig.9 The measured geological map of carbonic stratum by the profile drawing method with 3D projection at the southeast part of Qilin Mountain anticline,Fenghuang Mountain region,Chaohu City,Anhui Province |
|
图10 安徽巢湖市凤凰山地区麒麟山背斜东南翼石炭纪地层导线法实测地层剖面图 Fig.10 The measured geological map of carbonic stratum by the leading line method at the Southeast part of Qilin Mountain anticline,Fenghuang Mountain region,Chaohu City,Anhui Province |
导线法的二次二维投影绘制方式对常规导线和平移导线都造成了总导线方位上投影偏差,三维投影绘图方法从原理上解决了导线法的问题。通过 图 9和图 10的对比,可以看出三维投影法新确定的界线点与实际相符,在实测地层剖面中不再展现平移线,使图形易识读。而导线法与实际并不相符,可以预见填图后沿总导线方向的图切剖面应与 图 9相同,而与 图 10差别很大。
虽然三维投影法绘制过程相对繁琐,但计算机实现已弥补了该缺点(王兆国等,2015),图 9即为用计算机计算绘制结果。从绘制结果看,三维投影法与导线法相比具有明显优势,两者对比如 表 1所示。
| 表1 导线法与三维投影法的对比 Table 1 The differences between the leading line method and the profile drawing with 3D projection |
通过对导线法绘制方法的讨论,认识到导线法绘制的原理缺陷:
(1) 导线法二次二维投影绘制方式造成常规导线在总导线方位上确定的地层边界点并非实际的地层边界点。
(2) 导线法二次二维投影绘制方式与视倾角三维计算方式的差异性,造成了层面陡坎上的不同测量方式的导线均是平移线,并且使地形线与岩性线之间存在夹角。只有当计算得到的总导线方位与层面陡坎倾向一致,或总导线方位与层面上分导线方位一致时,才会出现岩性线与平移线重叠现象。
针对导线法的缺陷,本文提出了新的三维投影剖面绘制方法,从该方法的原理和实例可以看出该方法具有如下优势:
(1) 三维投影剖面绘制方法,解决了导线法二次二维投影对常规导线的影响,使得常规导线在总导线方位上确定的地层边界点为真实的地层边界点,且三维投影法绘制的地层剖面图与总导线方位上的图切剖面一致。
(2) 三维投影剖面绘制方法,从原理上解决了二次二维投影与视倾角三维计算的矛盾,使得平移导线只在导线平面图中展现,而不出现在地层剖面图之中,消除了地形线与岩性线之间存在夹角和平移导线处理多解性问题。
| [1] | 陈志军, 陈建国. 2012. 基于MapGIS的图切地质剖面系统面向对象设计与实现. 地质学刊, 36 (3): 256-264 . |
| [2] | Chen Zhijun and Chen Jianguo. 2012. Object orientation design and implementation for cutting section of geological map system based on MapGIS. Journal of Geology, 36 (3): 256-264. |
| [3] | 方世明, 刘刚, 赵温霞等. 2002. 地质图切剖面中褶皱构造的计算机辅助编绘. 地质与勘探, 38 (3): 52-54 . |
| [4] | Fang Shiming, Liu Gang, Zhao Wenixa et al. 2002. The drawing aided by computer of the anticline and syncline in the section from geological map. Geology and Prospecting, 38 (3): 52-54. |
| [5] | 郭福生, 林银山, 龙金花. 1999. 岩层真厚度计算公式述评——兼与佟再三、 佟洁、 许边远同志商榷. 中国煤田地质, 11 (2): 23-25 . |
| [6] | Guo Fusheng, Lin Yinshan and Long Jinhua. 1999. Review of formula for calculating the true thickness of strata. Coal Geology of China, 11 (2): 23-25. |
| [7] | 黄立华. 1986. 岩层厚度计算的新方法——矢量代数法. 地层学杂志, 10 (2): 148-152 . |
| [8] | Huang Lihua. 1986. A new method for the calculation of rock thickness: Vector algebra method. Journal of Stratigraphy, 10 (2): 148-152. |
| [9] | 李义才, 刘刚, 吴冲龙. 2001. 计算机辅助实测地质剖面图编绘系统设计. 地质通报, 20 (3): 304-308 . |
| [10] | Li Yicai, Liu Gang and Wu Chonglong. 2001. Design of the computer-aided geological section-making system. Geological Bulletin of China, 20 (3): 304-308. |
| [11] | 刘杰, 梁立恒, 王海鹏. 2009. MapGIS下图切地质剖面自动绘制方法探究. 测绘与空间地理信息, 32 (5): 52-54 . |
| [12] | Liu Jie, Liang Liheng and Wang Haipeng. 2009. Study on the method of auto-draw slice geological profile in MapGIS. Geomatics & Spatial Information Technology, 32 (5): 52-54. |
| [13] | 裴丽娜. 2011. 基于ArcEngine的灾害地质立体图图切剖面技术研究(硕士学位论文). 武汉: 中国地质大学. 1-69. |
| [14] | Pei Lina. 2011. Technology on Transverse Cutting Profile of the Three Dimensional Geological Hazard Maps Based on ArcEngine(Master's Thesis). Wuhan: China University of Geosciences. 1-69. |
| [15] | 漆树基. 1991. 利用袖珍计算器计算岩层真厚度. 地质通报, (2): 188-193 . |
| [16] | Qi Shuji. 1991. Calculation of the true thickness of strata by use of the pocket calculator. Geological Bulletin of China, (2): 188-193 |
| [17] | 沈忠悦. 1988. 一个通用的岩层厚度计算公式. 地质与勘探, 24 (1): 35-36 . |
| [18] | Shen Zhongyue. 1988. A common calculation equation of the strata thickness. Geology and Prospecting, 24 (1): 35-36. |
| [19] | 佟再三. 1983. 岩层真厚度计算之程序. 地质与勘探, 19 (11): 38-41 . |
| [20] | Tong Zaisan. 1983. The calculation procedure of the true strata thickness. Geology and Prospecting, 19 (11): 38-41. |
| [21] | 王兆国, 鲁如魁. 2015. 基于Fortran语言和GMT软件的实测地质剖面的迅速实现. 计算机应用, 35 (增刊2):301-304 . |
| [22] | Wang Zhaoguo and Lu Rukui. 2015. Rapid implementation of measured geological section based on Fortran language and GMT software. Journal of Computer Applications, 35 (suppl. 2): 301-304. |
| [23] | 王铸. 2009. 利用ActiveX Automation在AutoCAD中自动切取地质剖面. 工程地质计算机应用, (4): 32-38 . |
| [24] | Wang Zhu. 2009. Automatically cut the geological section in the AutoCAD software using ActiveX automation. Engineering Geology Computer Application, (4): 32-38. |
| [25] | 肖水清. 1977. 实测剖面上计算岩层厚度的方法. 地质与勘探, 13 (3): 50-52 . |
| [26] | Xiao Shuiqing. 1977. The calculation of the strata thickness in the measured geological section. Geology and Prospecting, 13 (3): 50-52. |
| [27] | 许边远. 1998. 试用矢量表示岩层真厚度. 地质通报, 17 (1): 80-86 . |
| [28] | Xu Bianyuan. 1998. The use of the vector in expressing the true thickness of strata. Geological Bulletin of China, 17 (1): 80-86. |
| [29] | 许明七. 1985. 求岩层真厚度的简易计算程序. 地质与勘探, 21 (9): 35-36 . |
| [30] | Xu Mingqi. 1985. The calculation precedure of the true strata thickness. Geology and Prospecting, 21 (9): 35-36. |
| [31] | 杨光忠, 胡永虹. 2002. 试论实测地质剖面的电算化处理. 贵州地质, 19 (1): 67-71 . |
| [32] | Yang Guangzhong and Hu Yonghong. 2002. Treatment of electronic calculation for measured geological sections. Guizhou Geology, 19 (1): 67-71. |
| [33] | 杨利容, 赖德军, 罗娟. 2011. 基于AutoCAD实测地质剖面数字成图关键技术. 物探与化探, 35 (2): 261-264 . |
| [34] | Yang Lirong, Lai Dejun and Luo Juan. 2011. The key technology for digital mapping of measured geological profile based on AutoCAD. Geophysical & Geochemical Exploration, 35 (2): 261-264. |
| [35] | 庄培德. 1983. 地层厚度计算方法的改进. 地层学杂志, 7 (2): 154-158 . |
| [36] | Zhuang Peide. 1983. The improvement of the calculation method of the strata thickness. Journal of Stratigraphy, 7 (2): 154-158. |
 2016, Vol. 51
2016, Vol. 51

