
2016第42卷第8期
2.上海财经大学 公共政策与治理研究院,上海 200433
2.Institute of Public Policy and Governance, Shanghai University of Finance and Economics, Shanghai 200433, China
近年来,关于我国延迟退休政策的讨论越来越受到人们的关注。支持延迟退休政策的人认为我国老龄化程度的加剧和人口预期寿命的增加使得延迟退休政策在可行性上得到支持,①并且有利于缓解养老基金支付压力。反对的人则认为延迟退休政策会对劳动力市场造成冲击,使得就业市场的形势更加严峻,并可能会对人们的福利造成损失。②从长期来看,延迟退休政策到底会对劳动力市场产生怎样的影响?又会对宏观经济产生怎样的冲击?是提高了还是降低了社会福利水平?如果实施延迟退休政策,需要配套什么样的辅助性措施?是降低养老保险缴费率还是提高养老保险待遇?这些问题的回答,不仅有助于我们理解延迟退休政策的利弊,更能够对今后的具体政策制定与实施提供理论或经验依据。为此,需要建立合适的分析框架,不仅能够分析延迟退休政策对养老金盈亏的影响,而且还要控制政策对劳动力市场的冲击等其他因素的影响,这是本文的理论意义所在。
①第六次全国人口普查数据显示,我国60岁及以上人口占比为13.26%,65岁及以上人口为8.87%;全国人口预期寿命为男性72.38岁,女性77.37岁,整体74.83岁。与此同时,我国目前的退休年龄基本沿用20世纪50年代的规定,男职工的退休年龄为60周岁,女职工为50周岁,女干部的退休年龄为55周岁。
如参见http://news.sina.com.cn/c/2013-07-26/010527773153.shtml。
在论证延迟退休的可行性问题时,有两个问题引起了人们的特别关注。一是延迟退休是否会恶化当前的劳动力市场,即由于老年人延迟退出劳动力市场,导致年轻人无法充分就业,挤压了年轻人的就业机会;二是随着年龄的提高,个体的劳动生产效率变低,延迟退休虽然会增加部分收入,但挤占了休闲,得不偿失。针对第一个问题,已有相关文献进行了分析讨论,并得出老年人的就业与年轻人的就业并不冲突的结论,如张川川、赵耀辉(2012)、Zhang Chuanchuan(2012)等使用1990年、2000年人口普查数据和2005年全国1%人口抽样调查数据考察了高年龄段人口就业对年轻人就业的影响,他们发现高年龄段人口就业的增加会提高而非抑制年轻人就业。Munnel和Yanyuan Wu(2012)也发现,在美国,老年人挤压年轻人的就业机会的情况是不存在的。针对第二个问题,提高退休年龄后,那些原本可以退休的人继续工作,但一方面由于此时个体的劳动边际回报率较低,收入效应带来的福利改善有限;另一方面由于工作挤占了休闲时间,而休闲的减少将直接导致个人效用的降低。由此可见,影响延迟退休政策效果的因素众多,在分析延迟退休政策时需要充分考虑这些情况。
在本文中,我们将综合考虑以上各种因素,通过建立一个大型的一般均衡世代交叠模型(Dynamic General Equilibrium Overlapping Generation Model)并引入退休年龄对劳动力市场的冲击来研究养老金延迟退休政策对城镇企业职工福利的影响问题。我国城镇职工基本养老保险中还包括机关事业单位职工的养老保险,但由于机关事业单位的养老保险改革于2015年刚刚启动,且其基金运行独立于现存企业职工养老保险基金,因此本文研究中,只分析城镇企业职工的基本养老保险问题,没有考虑机关事业单位的养老保险问题。我们不仅考虑了城镇企业职工在劳动力市场上面临的失业风险,还考虑了延长退休年龄对个体失业风险的内生作用。针对延迟退休的配套政策,我们分两种情况进行考察:一是保持现有的养老保险缴费率不变,调整退休人员的养老保险待遇;二是保持现有的养老保险待遇不变,调整个体的缴费率。相对于局部均衡模型和简单的一般均衡模型,我们所使用的大型一般均衡世代交叠模型能更好地刻画中国宏观经济状况及中国养老保险体制现状,并较准确地反映养老保险政策对城镇企业职工的福利影响。本文采用的分析框架对研究中国养老保险体制改革问题具有独特而重要的应用价值。
我们的研究发现,无论采取何种延迟退休方式,均可以提高城镇企业职工社会福利水平,但对宏观经济变量的影响不尽相同。如果采用保持现有的养老保险缴费率不变的方式,以中国目前劳动力市场的状态,从长期来看,延迟退休5年会使社会福利提高1.1%,社会总消费提高4.1%,产出增加1.9%,但资本产出比由于资本存量的减少而下降2.4%,这主要是因为在养老保险缴费率保持不变的情况下,延迟退休可以显著提高养老金待遇,养老金对储蓄的挤出效应明显,导致储蓄降低,资本存量下降;如果采用保持现有的养老保险待遇不变的形式,延迟退休5年会使社会福利提高3.7%,社会总消费提高8.3%,产出增加8.6%,资本产出比提高0.29%,这主要是因为在养老金待遇不变的情况下,养老保险缴费率会显著下降,养老保险缴费率对社会资源的扭曲显著减少。我们的研究还发现,劳动力市场的状态直接影响了延迟退休政策的福利效果。针对当前我国城镇失业率的统计一直有争议,如Giles,Park和Zhang(2005)估计的1999年之后的城镇失业率高达14.0%,Liu(2012)估计的失业率高达9.5%。根据我们的计算,如果当前的失业率为10%甚至更高的话,延迟退休带来的福利改进很小,并且最优的退休年龄也会相应降低,如在失业率为10%的情况下,最优的退休年龄为64岁。
自从Auerbach和Kotlikoff(1987)首次利用大型一般均衡世代交叠模型分析养老保险政策对经济系统的影响以来,该模型在有关养老保险政策研究中得到了广泛应用。mrohoroglu、Imrohoroglu和Joines(1995)通过引入收入的个体异质性冲击,把该模型推广到不完全市场的框架下,并藉此研究了美国养老保险的最优替代率和相应的社会福利问题。由于老龄化的冲击导致养老保险体系不可持续性成为世界性的问题,因此有越来越多的文献利用该不完全市场的分析框架分析了延迟退休政策对宏观经济、养老保险的可持续性以及社会福利的影响。①比如,Díaz-Giménez和Díaz-Saavedra(2009)分析了西班牙延迟退休政策产生的影响,他们发现,延迟退休三年的政策足够解决西班牙养老金的可持续性问题,并且全社会的福利水平还得到了改善;Imrohoroglu和Kitao(2012)通过在模型中引入了健康风险,并且同时考虑了劳动工作时间与劳动参与率的影响,分析了美国可行的养老保险改革政策,他们发现延迟退休两年可以显著提高劳动供给与资本存量;Kitao(2014)分析了美国在人口老龄化的背景下如何保持养老保险的可持续性,她的研究发现将退休年龄提高到73岁便可以解决养老保险的可持续性问题。
①Song,Storesletten,Wang和Zilibotti(2015)则采用了Auerbach和Kotlikoff(1987)建立的完全市场分析框架,针对中国养老保险现状,分析了在经济高速增长和人口老龄化背景下如何发挥养老保险政策的再分配功能,使得所有人都能分享改革成果。本文与Song等人(2015)的区别主要有两点:一是本文采用的研究框架是不完全市场一般均衡模型,经济体中的个体会面临个体异质性收入冲击,而Song等人(2015)的分析框架是一个完全市场模型;二是本文主要集中于延迟退休政策对经济体和社会福利的影响,而Song等人(2015)则主要关注养老保险的再分配职能。
国内学者关于养老保险方面的研究主要是通过实证方法分析养老保险政策对个体行为的影响。例如,Feng,He和Sato(2011)针对中国1997年和2005年的两次养老保险改革,分析了养老保险对家庭储蓄行为的影响,并且进一步指出了养老金下降会显著降低家庭对教育和健康的消费;白重恩、吴斌珍和金烨(2012)探讨了养老保险缴费对家庭消费的抑制作用,研究指出在给定缴费前的收入水平和养老保险覆盖状态时,提高养老保险缴费率会显著抑制缴费家庭的消费;何立新、封进和佐藤宏(2008)利用DID的方法分析了1997年养老保险改革对家庭储蓄的影响,指出养老金财富对家庭储蓄存在显著的替代效应;何立新(2008)研究了1997年和2005年我国养老保险体制改革产生的收入分配效应,指出两次改革产生了完全不一样的收入分配效应。徐舒、赵邵阳(2013)在局部均衡的框架下分析了养老金“双轨制”对公务员和城镇企业职工生命周期消费差距的影响。
本文的研究与上述文献存在三方面区别:首先,在研究内容上,本文关注的是如何预估延迟退休政策可能产生的福利效果,而一般实证方法(如DID方法)只能分析已发生政策的影响;其次,在研究方法上,本文通过在生命周期模型中引入摩擦,控制了退休年龄对劳动力市场的影响,与传统的对个体异质性收入冲击的建模相比,能够捕捉延迟退休政策对劳动力市场的影响,更符合中国的情况;最后,在分析框架上,本文采用了一般均衡的分析框架,相比较于会计模型与局部均衡模型,可以控制政策变动对利率和工资率的影响,更符合卢卡斯批判,得到的结论更精确。
文章后续结构如下:第二部分介绍了分析所用的模型组成;第三部分描述了参数校准的过程和基准模型的性质;第四部分讨论了延迟退休政策的结果分析;最后是本文的结论。
二、 模型在本节中我们将建立一个完美预期的不完全市场经济世代交叠模型。在此经济中,政策变量是外生的,并可以被经济中所有个体完美预测。这个经济由处于不同年龄段的个体组成,每个个体都是价格接受者,在劳动力市场中每年都受到一个外生的、个体异质性的收入冲击。收入冲击在模型中具体表现为:不论个体当期是否处于就业状态,在下一期都有π的可能性失业和1-π的可能性就业。面临这样的收入冲击,个人选择最优化的消费和储蓄路径来最大化其终生期望效用。劳动力市场也是有摩擦的,失业概率是内生的,由当期劳动力市场中的总人数决定。我们的基准模型主要包括以下几个部分:
(一) 人口结构模型中在每一时期都包括了相互独立、测度为1的连续个体,人口的增长率为外生的,设为n。个体在J0岁时进入劳动力市场,一直工作到JR岁时退休,在J岁时死亡。在每个时期,年龄为j的个体都只有ψj的概率存活到下一期,所以个体从开始进入经济活到期的无条件生存概率为
| $ {\mu _j}={\psi _{j-1}}{\mu _{j-1}}/\left({1 + n} \right), \sum\nolimits_{j=1}^J {{\mu _j}=1} $ |
每个个体在进入经济系统时都没有资本,仅有1单位的劳动可以用来工作或休闲,个体可以从消费与休闲中获得效用,在生命周期上其一生的效用可以写成如下形:
| $E\left\{ {\sum\limits_{j=1}^J {{\beta ^j}\left({\Pi _{i=1}^j{\psi _i}} \right)u\left({{c_j}, {l_j}} \right)} } \right\}$ | (1) |
其中:β为贴现因子,
在模型中,企业为一个代表性厂商,在每期雇佣劳动和租赁资本进行生产。假设企业有一个规模报酬不变的生产函数,为Cobb-Douglas形式:
| $ {Y_t}={A_t}K_t^\alpha L_t^{1-\alpha } $ |
其中:At表示t期经济中的技术水平,Kt表示企业租赁的资本,Lt表示企业雇佣的劳动。资本的累积过程为Kt+1=(1-δ)Kt+It,其中δ表示资本的折旧率,It表示t期的投资。根据企业的利润最大化行为,可以得到市场上的利率水平和工资水平分别为:
| ${r_t}=\alpha {A_t}K_t^{\alpha-1}L_t^{1-\alpha }-\delta$ | (2) |
| ${w_t}=\left({1-\alpha } \right){A_t}K_t^\alpha L_t^{-\alpha }$ | (3) |
在模型中,政府运营一个收支平衡的失业保险体系和一个收支平衡的养老保险体系。而对中国的养老保险体系,根据孙祁祥(2001)和Sin(2005)等人的研究,我国目前养老保险中的个人账户基本是空账,所以我们在模型中没有考虑个人账户。在本文中,我们假定政府设定好个体的养老保险收益,然后再通过养老保险缴费来保证收支平衡。政府规定的个体养老金待遇为:
| $S{S_{it}}=\theta \left({\lambda {{\bar W}_t} + \left({1-\lambda } \right){Q_i}} \right)$ | (4) |
其中:SSit表示个体i退休后在第t期拿到的养老金待遇,θ表示养老金替代率。
当一个年轻个体进入经济系统,给定她当前的工作状态和拥有的资产,她将面临一个异质性的生产冲击,使得她在下一期可能拥有工作机会也可能没有工作机会;若个体当期有工作,则她的工资收入由两部分组成:一部分是市场出清工资,一部分为个体的年龄效率参数(age-wage profile),但还要扣除养老保险缴费与失业保险缴费;若个体当期没有工作,则只能拿失业保险。并且由于在经济系统中,每个个体都不能确定地存活到下一期,总会有一些人亡故,政府将这些人的资产收集起来重新分配给每个存活的个体,定义为beg。因此一个在劳动力市场的个体选择问题可以描述为:
| $\begin{aligned}v\left({{a_j}, {s_j}} \right)={\text{Max}}\left\{ {u\left({{c_j}, {l_j}} \right) \\+ \beta {\psi _{j + 1}}Ev\left({{a_{j + 1}}, {s_{j + 1}}} \right)} \right\}\end{aligned}$ | (5) |
| $ \begin{gathered} s.t.\; \;{a_{j + 1}} + {c_j} =(1 + r){a_j} + {q_j} + beq \hfill \ \\ {q_j}=\left\{ \begin{gathered} (1-{\tau _{ss}}-{\tau _u})w{\varepsilon _j}\left({1-{l_j}} \right)\; \;\; \;\; if\; \;s=e\\ \hfill \ UI\quad \quad \quad \quad \quad \quad \quad \; \;\; \;\; \;\; \;\; if\; \;s=u \hfill \ \end{gathered} \right. \hfill \ \end{gathered} $ |
在退休前一年,由于下一期个体将退出劳动力市场,不会再受到来自劳动力市场的个体异质性冲击,因此个体选择问题变为
退休后,个体将不再提供劳动,收入只能依赖于养老金和个人的储蓄,并且在最后一期,根据个体的最优化行为,个体将会把所拥有的资产全部消费掉,不再拥有资产。因此此时个体的选择问题变为
根据Shimer(2011)的研究,我们假定在经济中,劳动力市场是有摩擦的,具体表现为均衡失业率由当期工作人员的比例决定。假定当期的失业人口比例为ut,就业人口为et,总人口为lt,则lt=ut+et。失业人员找到工作的概率(job finding rate)为ft,就业人员失去工作的概率(job separation rate)为λt,那么关于下一期的失业率我们就有如下公式:
| $\begin{aligned} {u_{t + 1}}= & {u_t}\left({1{\text{-}}{f_t}} \right){\text{ + }}{e_t} \times {\lambda _t} \hfill \ {u_{t + 1}}-{u_t} \\= & {e_t} \times {\lambda _t}-{u_t} \times {f_t} \hfill \ \end{aligned} $ | (6) |
即下一期的失业率由两部分组成,一部分是当期的失业人员中没有找到工作的部分,另一部分是当期有工作的人员失去工作的部分。
如果劳动力市场是稳定的,我们有
为了分析延迟退休政策的宏观影响与福利效果,我们首先要确定模型的各个参数。在这些参数中,有些可以根据现有文献和中国经济数据得到,我们把这类参数称为外生参数;有些需要通过校准,使模型产生的数据与现实数据相吻合而获得,我们把这类参数称为内生参数。文章先介绍外生参数的设定值与选取原则,再给出内生参数的取值与取值原则。在给定模型的参数后,我们将检验基准模型是否可以描述中国经济的一些特征,以确保模型的适用性,我们基准模型的对象数据为2010年的中国经济体。
(一) 外生参数设定1.人口参数的设定。我们假定个体在20岁进入劳动力市场,60岁退休,90岁死亡退出经济体。根据《中国统计年鉴2011》,1997-2011年间的人口平均年增长率只有0.64%,由于我们的分析主要集中于城镇企业职工,并且考虑到农村人口向城市的转移,所以我们将人口增长率设为1%。①由于我国目前没有公布最新的生命表,无法直接得到条件生存概率,我们将根据2010第六次全国人口普查数据推算得到条件生存概率。
①我们对人口增长率为0.6%-1.5%的设定值均作了模拟,发现对我们的主要结论没有影响,限于篇幅限制,此处仅给出了基准模型的结果,有兴趣者可向我们索取完整结果。
2.养老金参数的设定。根据1997年的养老金体制改革规定,企业职工的养老金统筹账户和个人账户设定的目标替代率为60%,所以本文中将企业职工的替代率设为0.6;根据Sin(2005)的研究,中国各个省份的λ均不相同,大概范围在0.4-0.6之间,在本文中将λ设为0.6,使企业职工可以更大限度地分享经济增长成果。企业职工还需要为养老保险缴费,缴费率由模型根据收益准则内生产生。
3.工资增长率的设定。根据Ge和Yang(2013)的测算,在控制了人力资本的情况下,2000-2011年间中国的人均工资增长率约为5.8%。所以本文中工资增长率设为5.8%。
4.资本产出弹性和折旧率的设定。由于缺少历年存量资本的数据,并且从统计数据中反推出存量资本的方法不同,导致各种研究对资本产出弹性和折旧率的估计也不相同。在本文中,资本产出弹性和折扣率的选取均参考Bai、Hsieh和Qian(2006)的做法,将α设为0.5,资本折旧率δ设为10%。
5.年龄效率参数(Age Efficiency Profile)的设定。我们利用2007年CHIPS数据来估计企业职工的年龄效率参数。遵循文献中的一般设定,②采用明瑟收入函数(Mincerian income function)型的工资方程有:③
| $ \ln (wage)={\beta _0} + {\beta _1}age + {\beta _2}ag{e^2} + other + \varepsilon $ |
②具体文献可参见Chamon,Liu和Prasad(2013)以及Heathcote,Storesletten和Violante(2010)。
③在回归方程中,wage表示个体的月收入,age表示个体的年龄。其他控制变量包括个体的性别、职业、工作性质、单位所有制性质和省级哑变量。我们在回归时所选人群为“具有城市户口的年龄在18岁以上,男性60岁以下,女性55岁以下的有工作的个体。”
其中:可以由exp(β1age+β2age2)推算出个体的年龄效率参数。
6.劳动市场参数的设定。在本文中,失业风险是个体异质性冲击的主要来源,在基准模型中,我们仿照mrohoroglu(1995)等的设定,假定无论企业职工当期是否有工作,下一期都以96%的概率得到一份新工作,以4%的概率失业,此处的4%是中国城镇企业职工的长期失业率。在退休年龄改变后,失业概率也会随之变动。失业保险缴费率设定为3%,失业保险的替代率将内生决定。④
④本文还考虑了另外一种失业保险的设定方式。即参照陈彦斌、霍震和陈军(2009)的研究,将失业保险替代率设定为0.07,失业保险缴费率由模型内生决定,结果可向作者索取。
| 系数 | RSE | |
| 注:(1)*、**和***分别代表 10%、5%和1%的显著性水平;(2)由于篇幅限制,我们仅汇报了与本文相关的变量的回归结果,有兴趣者可向作者索取全部回归结果。 | ||
| 年龄 | 0.0313*** | 0.00601 |
| 年龄的平方 | -0.000433*** | 0.0000767 |
| 教育等级 | 0.318*** | 0.0273 |
| 省份哑变量 | Yes | - |
| R-squared | 0.382 | - |
| N | 6 155 | - |
在本文中,内生参数主要是三个效用函数参数。我们通过资本产出比来校准β。我们首先以1952年为基年(参考张军和章元(2003)及所引用的参考文献),通过永续盘存法测算了从1952年至今的资本产出比,并计算了2010-2012年间的平均值(约为2.8)。我们通过调整β的数值使模型的资本产出比与实际值(即2.8)相吻合,得到β=1.01;为了校准v,我们首先根据CHIPS(2007)中个体劳动时间数据来测算个体平均工作时间占总可支配时间的比例,其结果为0.40,①然后通过调整使模型产生的平均工作时间与实际值(即0.40)相符合,得到v=0.37。最后,我们遵循文献的一般设定选取σ=1.5,对应的相对风险规避系数(RRA)为1.36(一般宏观文献取值范围在1-4之间)。②
①具体年化规则为:每周工作时间/7/16,即假定一周有七天,每天16小时可供支配(除去8小时睡眠时间)。
②参见Cooley和Prescott(1998)或Auerbach和Kotlikoff(1987)对如何选取相对风险规避系数的讨论。我们也针对σ的不同取值分别作了稳健性检验,发现对我们的主要结论没有影响。
(三) 基准模型的适用性上节我们给出了本文模型参数的取值及其选取依据,现在我们考察基准模型的适用性。表 2报告了模型所产生的经济变量数值与真实经济变量数值的比较。显然,作为校准依据的变量,资本产出比和平均工作时间十分符合。关于中国的利率水平目前的文献还没有定论,例如郭新强和胡永刚(2012)的文章指出,从1992年到2010年一年期的贷款利率的平均水平为7.93%;汪伟、郭新强和艾春荣(2013)采取的1992-2008年间中国名义存款利率为3.45%;本文中模型产生的利率为7.8%,在可接受范围之内。根据《2013中国统计年鉴》的数据显示,2007年之后,中国的国内总储蓄率已经高于50%,2007-2012年间平均储蓄率为51.1%,与模型产生的47.4%接近。虽然政府规定的缴费率为28%,③但根据Song等人(2015)的研究,由于存在逃避缴纳等情况,真实的缴费率为20%左右,模型所产生的缴费率为23.08%,介于20%-28%之间。④由此可见,我们的基准模型可以很好地描述中国宏观经济状况。
| 变量描述 | 模型数据 | 真实数据 |
| 资产产出比 | 2.81 | 2.8 |
| 平均工作时间 | 0.404 | 0.4 |
| 缴费率 | 23.08% | 20%-28% |
| 利率 | 7.8% | 3.45%-7.93% |
| 国民储蓄率 | 47.4% | 51.1% |
③由于本文中没有考虑个人账户,所以养老保险缴费为统筹账户缴费率20%与个人账户缴费率8%之和。
④如果不考虑个人账户,实际缴费率只有20%的情况下,目前养老保险已经不能维持可持续性,由此也可以看出,在未来老龄化越来越严重的情况下,我国养老保险体系面临着很严重的可持续性问题。
由于模型中的养老保险系统具有自我融资(Self-Finance)的性质,即缴费率只能由模型内生决定,因此,养老保险总是收支平衡的。虽然如此,但从模型生成的缴费率看,仍然可以部分说明目前养老保险基金的困境。
根据规定,我国养老保险分为统筹账户与个人账户,其中单位缴费率为20%,缴费资金进入统筹账户;个人缴费率为8%,缴费资金进入个人账户。从经济学意义上讲,单位所缴费用也是用工成本的一部分,最终也可以看作由个体承担,而模型产生的缴费率为23.08%。这说明如果个人账户为空,即统筹账户的总缴费率为28%,则表明目前的养老基金还有剩余,⑤但如果个人账户做实,即统筹账户的总缴费率为20%,则表明目前统筹账户确实面临亏空的风险,需要用额外的资源来抵消这一部分亏空(即多出的3.08%缴费率)。
⑤如根据人力资源与社会保障部的数据显示,2014年年末基本养老保险基金累计结存35 645亿元。养老保险基金并不亏空。
这一结论也与围绕养老保险基金究竟是否亏空的争论相符,即虽然一直有部分专家学者说养老保险基金有盈余,但仍有很多专家学者认为养老保险基金面临很大的收支困难。另一方面,这一结论也为延迟退休政策提供了很好的背景与目的依据。
四、 结果分析通过上述对基准模型的分析可以看出,本文的模型可以反映当前的中国经济和养老保险状况。在此基础上,我们通过修改基准模型中的退休年龄和养老保险政策参数,同时利用反事实实验的方法探讨延迟退休对个体福利水平和宏观经济因素的影响。首先,我们给出个体福利的定义,通常情况下,个体的福利水平被定义为:一个新进入经济体的个人所能获得的最大效用。可是,模型所产生出来的效用值,只有大小顺序意义,没有经济学含义。因此,在衡量福利得失多少时,本文采用消费等价量(CEV,Consumption Equivalent Variation)。CEV的表达式为:
从前文关于养老保险政策的描述中可以看出,由于养老保险是收支平衡的,所以缴费率与收益准则只能改变其中一个,另一个则由模型内生产生。因此,在本节中,我们在分析时考虑了两种不同的延迟退休配套措施:一种是保持现有缴费率不变,改变养老保险的收益准则,通过调整养老金替代率,从而使养老保险达到收支平衡;另一种是保持养老保险的收益准则不变,通过改变养老保险的缴费率,从而使养老保险达到收支平衡。本文利用企业职工生命周期中各个变量的变化作为微观基础,来分析政策改变怎样影响个人的选择,进而对整个宏观经济产生影响。在以下的分析中,我们主要展示了初始失业率为4%、7%和10%的情况。①
①其他结果与这三种情况类似,若需要可通过邮件向作者本人索取。
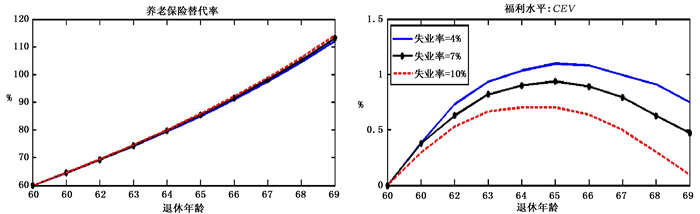
(一) 缴费率不变图 1描述了缴费率保持不变情况下延迟退休对福利水平的长期影响以及相对应的养老保险替代率,图 2描述了缴费率保持不变情况下延迟退休对宏观经济因素的影响。可以看出,如果保持缴费率不变,延迟退休会从两种渠道影响养老金替代率:一是随着退休年龄的提高,需要供养的老年人在逐渐减少,而提供劳动的个体在逐渐增加,导致老龄社会抚养比②在不断下降,替代率不断上升;二是社会平均工资和个体平均工资会随着退休年龄的提高而下降,这也会导致养老保险替代率会随着退休年龄的提高而提高,甚至在退休年龄提高到68岁时超过了100%。而影响社会平均工资的因素主要有如下三点:首先,虽然个体工资在工作期的前期会随着年龄的增加而增加,但在40岁左右达到顶峰后逐渐下降(见图 1(a));③其次,个体的工资也会受个体的劳动供给的影响,即由于老年期个体的劳动供给相对较低,结果导致劳动收入降低;最后,延迟退休也会提高社会总劳动供给,从而增加劳动力市场的竞争,降低市场出清工资。在我们的分析中,后两种影响控制了第一种影响,因此会导致社会平均工资和个体平均工资降低。
②老年抚养比表示老年人口与劳动年龄人口之比。
③这也与劳动经济学中关于劳动收入的研究结论一致,在分析劳动收入时,一般年龄(或经验)对劳动收入的影响为正,但年龄的平方(经验的平方)对劳动收入的影响却为负。可见尹志超、甘犁(2009)等的研究。
|
| 图 1 缴费率不变下的福利水平与替代率 |
|
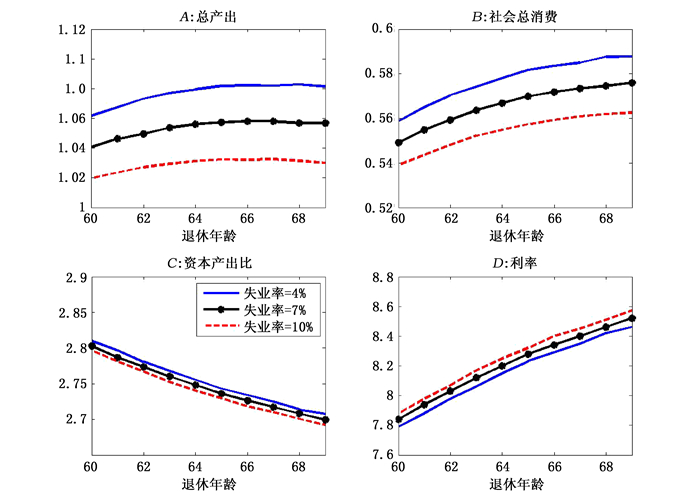
| 图 2 缴费率不变下的宏观经济总量 |
而在社会福利方面,影响个体福利水平的因素主要有两个:(1)缴费率的扭曲作用。由于缴费率保持不变,缴费率对延迟退休前即在劳动力市场的个体扭曲不变,但对那些由于延迟退休政策重新进入劳动力市场的人扭曲增加,①这会降低个体的福利水平;(2)随着养老金替代率的提高,养老保险的风险共享(risk sharing)机制②变得越来越强,会提高个体的福利水平。综合来看,养老保险的风险共享作用占据了主导地位,延迟退休从长期来看会带来福利改进,但随着退休年龄的提高,缴费率的扭曲作用越来越大,导致继续增加退休年龄反而会导致福利的下降,可以看出,在初始失业率为4%和7%的情况下,延迟退休5年会达到福利最大化,在初始失业率为10%的情况下,延迟退休4年会达到福利最大化。并且我们还发现,初始失业率越高,延迟退休带来的福利改进越有限。
①以初始失业率为4%,退休年龄从60岁调整到61岁为例,对60岁的个体, 面临的边际缴费率从0%上升到23.08%。
②风险共享是指是个体面临的风险可以通过在全社会的资源再分配得到风险分担。
下面我们继续分析延迟退休政策对宏观经济总量的影响。在总产出方面,首先由于缴费率保持不变,养老金待遇升高,个体为养老进行的储蓄减少,导致资本存量降低;其次,退休年龄增加会导致劳动总供给增加,在本文中,劳动供给增加的影响控制了资本存量的减少,导致总产出略微上升,如延迟退休5年只会是使总产出增加1.9%。在消费方面,总产出增加的“收入效应”会增加消费;此外,对重新进入劳动力市场的个体而言,休闲成本的上升引起的“替代效应”也会增加消费,因此总消费增加4.1%。在资本产出比方面,由于资本存量减少,产出增加,导致资本产出比下降2.4%。在利率方面,劳动总供给的增加会增加利率,资本存量的下降也会增加利率,两方面的因素导致利率上升了5.6%。
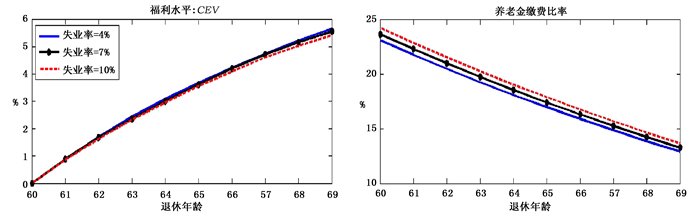
(二) 收益基准不变图 3描述了养老金待遇基准保持不变情况下延迟退休对福利水平的长期影响以及相对应的缴费率,图 4描述了养老金待遇基准保持不变情况下延迟退休对宏观经济因素的影响。可以看出,随着退休年龄的提高,缴费率在逐渐下降。这主要由以下两方面因素导致:(1)随着更多老年人进入劳动力市场,社会平均工资与个体平均工资下降,即使养老金的收益基准不变,但退休人员拿到的养老金绝对值在减少;(2)延迟退休导致领取养老金的老人减少,而需要缴纳养老金的个体则增加。两方面因素导致缴费率显著下降,从退休年龄为60岁时的23.1%下降到65岁时的17.0%。
|
| 图 3 收益准则不变下的福利水平与替代率 |
|
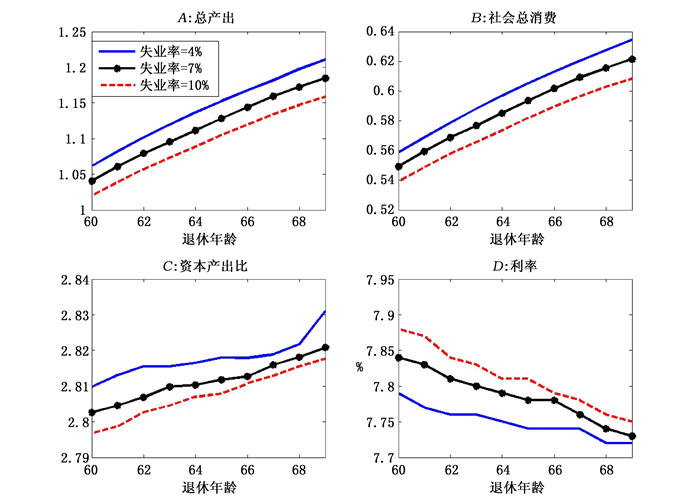
| 图 4 收益准则不变下的宏观经济总量 |
在社会福利方面,个体的福利水平一直在提高,主要原因为缴费率的扭曲作用减弱,由于缴费率在逐渐降低,缴费率虽然对那些由于延迟退休政策重新进入劳动力市场的个体扭曲增加,但是对延迟退休前即在劳动力市场的个体扭曲则显著变小,这会显著增加个体的福利水平,延迟退休5年使个体福利增加了3.7%。并且比较收益准则不变情况下的福利水平与缴费率不变情况下的福利水平可以发现,在延迟退休的同时,保持收益基准不变,适当降低缴费率会带来更大的福利改进。
在总产出方面,首先,虽然养老金待遇基准不变,但养老金待遇随着社会平均工资和个体平均工资的降低而降低,个体为养老进行的储蓄增加,导致资本存量增加;其次,由于缴费率在显著下降,缴费率对劳动供给的扭曲减小,延迟退休本身就会增加劳动总供给,因此劳动总供给会随着退休年龄的提高而增加,两方面的因素均使得产出增加,延迟退休5年会使总产出增加8.6%。在消费方面,同“缴费率保持不变”的情况相类似,总产出增加的“收入效应”会增加消费;此外,对已经在劳动力市场的个体而言,缴费率下降引起休闲成本下降,休闲成本的“替代效应”会降低消费。而对重新进入劳动力市场的个体而言,休闲成本的上升引起的“替代效应”会增加消费,三方面因素的共同影响导致总消费增加8.3%。在资本产出比方面,资本存量增加,产出也增加,而在本文中,资本存量的增加控制了产出的增长,导致资本产出比上升了0.29%。在利率方面,劳动总供给的增加会增加利率,资本存量的上升也会降低利率,两方面因素一增一减,最终导致利率下降了0.66%。
五、 结论本文在动态一般均衡世代交叠模型框架下通过引入异质性消费者分析了延迟退休政策对企业职工福利水平的长期影响。为了控制延迟退休对中国劳动力市场的影响,本文在劳动力市场中引入了摩擦,从而使失业率内生化。本文的分析表明,无论是采用保持现有的缴费率不变的方式还是采取保持养老金待遇不变的方式,延迟退休均能提高城镇企业职工的社会福利水平;最优的退休年龄与劳动力市场状态息息相关,如果当前就业形势严峻,最优退休年龄需要相应降低。
本文在三个方面对国内既有文献进行了扩展:一是采用了一般均衡分析框架,捕捉了政策改变后利率、工资等价格的改变,相对于局部均衡价格不变的假设,对政策效果的分析更精确,也会满足宏观经济学上的卢卡斯批判;二是在模型中引入了带有摩擦的劳动力市场,不但可以更好地描述中国现实,而且能够分析政策对劳动力市场的影响;三是构建了一个90期的大型世代交叠模型,这极大拓展了国内文献通常采用的三期模型,更能描述真实经济,该大型一般均衡世代交叠模型在国内关于生命周期理论的研究中尚未被使用,对后续研究有较强的借鉴意义。
本文还具有很强的政策意义:首先,实施延迟退休政策时有必要采取调整养老金待遇或降低缴费率等配套措施,并且相较于保持缴费率不变调整养老金待遇,保持养老金待遇不变的同时适当降低缴费率的配套政策可以带来更大的福利改进。其次,我们在分析延迟退休政策时,假定养老保险系统是收支平衡的,因此在提高退休年龄的同时还需要同时调整养老金待遇或缴费率,无论是养老金待遇的提高还是缴费率的降低均可以抵消延迟退休对休闲挤占的负面影响。但在现实中,提高退休年龄的同时可能并不会调整养老金待遇或缴费率,那么延迟退休的福利改进就受到了限制。本文所计算的福利改进程度就可以看作政策改进带来的福利改进的最高值。
| [1] | 白重恩, 吴斌珍, 金烨. 中国养老保险缴费对消费和储蓄的影响[J].中国社会科学,2012(8):48–71. |
| [2] | 陈彦斌, 霍震, 陈军. 灾难风险与中国城镇居民财产分布[J].经济研究,2009(11):144–158. |
| [3] | 郭新强, 胡永刚. 中国财政支出与财政支出结构偏向的就业效应[J].经济研究,2012(增2):5–17. |
| [4] | 何立新, 封进, 佐藤宏. 养老保险改革对家庭储蓄率的影响:中国的经验证据[J].经济研究,2008(10):117–130. |
| [5] | 何立新. 中国城镇养老保险制度改革的收入分配效应[J].经济研究,2007(3):70–91. |
| [6] | 孙祁祥. "空账"和转型成本——中国养老保险改革的效应分析[J].经济研究,2001(5):20–27. |
| [7] | 汪伟, 郭新强, 艾春荣. 融资约束、劳动收入份额下降与中国低消费[J].经济研究,2013(11):100–113. |
| [8] | 徐舒, 赵邵阳. 养老金"双轨制"对城镇居民生命周期消费差距的影响[J].经济研究,2013(1):83–98. |
| [9] | 尹志超, 甘犁. 公共部门和非公共部门工资差异的实证研究[J].经济研究,2009(4):129–140. |
| [10] | 张川川, 赵耀辉.延迟退休年龄会挤出年轻人就业吗? [R]. University Library of Munich, Germany, 2012. |
| [11] | 张军, 章元. 对中国资本存量K的再估计[J].经济研究,2003(7):675–699. |
| [12] | Auerbach A J, Kotlikoff L J. Dynamic fiscal policy[M]. Cambridge: Cambridge Univ. Press, 1987 . |
| [13] | Bai C E, Hsieh C T, Qian Y Y. The return to capital in China[J].Brookings Papers on Economic Activity,2006(2): 61–88. |
| [14] | Chamon, Marcos, Liu K, Prasad E. Income uncertainty and household savings in China[J].Journal of Development Economics,2003,105 164–177. |
| [15] | Cooley T F, Prescott E C. Economic growth and business cycles[A]. Cooley T F. Frontiers of business cycle research[C]. Princeton, NJ: Princeton University Press, 1998. |
| [16] | Díaz-Giménez J, Díaz-Saavedra J. Delaying retirement in Spain[J].Review of Economic Dynamics,2009,12(1): 147–167. |
| [17] | Feng J, He X L, Sato H. Public pension and household saving: Evidence from urban China[J].Journal of Comparative Economics,2011,39(4): 470–485. |
| [18] | Ge S Q, Yang T D. Changes in China's wage structure[J].Forthcoming in the Journal of the European Economic Association,2013 . |
| [19] | Giles J, Park A, Zhang J W. What is China's true unemployment rate?[J].China Economic Review,2005,16(2): 149–170. |
| [20] | Heathcote J, Storesletten K, Violante G L. The macroeconomic implications of rising wage inequality in the United States[J].Journal of Political Economy,2010,118(4): 681–722. |
| [21] | mrohoroglu A, Imrohoroglu S, Joines D H. A life cycle analysis of social security[J].Economic theory,1995,6(1): 83–114. |
| [22] | Kitao S. Sustainable social security: Four options[J].Review of Economic Dynamics,2014,17(4): 756–777. |
| [23] | Liu Y. Labor market matching and unemployment in urban China[J].China Economic Review,2013,24 108–128. |
| [24] | Munnell A H, Wu A Y Y. Will delayed retirement by the baby boomers lead to higher unemployment among younger workers? [R]. Boston College Center for Retirement Research Working Paper 2012, 2012-22. |
| [25] | Shimer R. Reassessing the ins and outs of unemployment[J].Review of Economic Dynamics,2012,15(2): 127–148. |
| [26] | Sin Y. China: Pension Liabilities and Reform Options for Old Age Insurance[R]. World Bank Working Paper, 2005, No. 2005-1. |
| [27] | Song Z M, Storesletten K, Wang Y, et al. Sharing high growth across generations: Pensions and demographic transition in China[J].American Economic Journal: Macroeconomics,2015,7(2): 1–39. |
| [28] | Zhang C C, Zhao Y H. The relationship between elderly employment and youth employment: evidence from China[R]. MPRA Paper, No. 37221, 2012. |

