双螺杆挤出机输送效率高而且稳定,对于物料的处理更均匀,是塑料等高聚物生产的重要设备,因此双螺杆挤出机内部聚合物流体的流动性态和数值模拟是一个热门的研究课题。
双螺杆挤出机内部的流体流动满足的数学模型是三维的非牛顿流体动力学方程组,区域复杂且随时间变化,因此是求解难点,通常直接采用有限元[1-3]等方法或将数学模型降维的方法来进行流体流动的数值求解,但缺点是难以精确有效。在此流体区域上求解双螺杆挤出机挤出问题的另一个重要途径是先将求解区域规则化,并在这个规则区域上进行流体计算。通常来说双螺杆挤出机流体流动区域的截面是一个三连通区域,有3个边界:外边界是一个类似于8字形的外边界,2个内边界是两根螺杆的截面边界。因此用合适的区域变换方法将螺槽区域变成规则化的区域,将大大简化对双螺杆挤出机流体的计算。
将一个截面在一个转动周期中不同时刻的区域形状经过规则化变换变为相同的圆界区域,再将双螺杆挤出机流体流动区域的截面转化成圆界区域后,求解区域非但不受时间影响,还变成了规则的、截面为三连通圆界(形状)区域的柱体,从而克服了求解双螺杆挤出机流体流动问题的主要困难。文献[4-6]研究了用区域变换方法求解单螺杆挤出机的流体流动问题,但其采用的方法只适用于双连通区域同心的情况,因此需要寻找更合适的共形映射方法来解决三连通区域的变换问题。
多连通区域的共形映射的计算方法有多种[7-9],通常是将区域映射到圆缝[7-8]。本文采用文献[9]的方法将三连通区域映射到圆界区域,同时对其算法的约束条件进行修改,以保证同一杆长位置不同转角的截面均映射到同样的圆界区域,并更正了其中共轭调和函数求解方程式的错误。为了验证共形映射算法的可行性,本文以内部边界曲线是两个椭圆的双螺杆挤出机流体流动区域为例求解该时变区域上的热传导方程的定解,并将数值解与精确解进行比较。计算结果表明,两解的绝对误差较小,可以用于求解双螺杆挤出机内部流体流动问题。
1 共形映射的计算 1.1 共形映射方法的理论公式本文使用并改进文献[9]的方法。首先考虑一个多边相连的有界平面区域Ωa,其边界分量是光滑的曲线。Ωa共形等价于圆界区域Ωc。设f: Ωa→Ωc为共形映射,同时令函数u=ln|f′(z)|,则u是Ωa上的调和函数,并且满足边界条件(1)
| $ \frac{{\partial u}}{{\partial n}} = - X\left( s \right) - 2\pi r_{\rm{v}}^{ - 1}{{\rm{e}}^u} $ | (1) |
式中,n是边界分量,rv是对应的圆界边界Ωc的半径, s是弧长参数,X(s)是Ωa的曲率,其值取决于s位于哪个边界上。
在区域边界有尖角的情况下,将区域记为Ωp。式(1)中X(s)在每个尖角的值是δ函数的倍数, 即X(s)=βδ(s),其中β是尖角的补角。所以共形映射f(z)可以近似表示为
| $ f\left( z \right) = {f_1}\left( {{{\left( {z - {z_0}} \right)}^\alpha }} \right) $ |
式中z0是尖角点的坐标,f1是一个单值解析函数,α=π/(π-β)。因此可以得到
| $ \ln \left| {f'\left( z \right)} \right| = \left( {\alpha - 1} \right)\ln \left| {z - {z_0}} \right| + w $ | (2) |
式(2)中w为调和函数的光滑部分。式(2)表明调和函数u在尖角部分有对数奇点,如果减去u中所有奇异部分,剩余部分即为在边界上光滑的调和函数。利用公式(3)可以得到与尖角部分有相同奇点的单值函数
| $ {\left( {\frac{{z - {z_0}}}{{z - {z^*}}}} \right)^{\alpha - 1}} $ | (3) |
式(3)中, z*是Ωp区域外部线段z0z*上除z0外的一点,从调和函数u中去除所有奇点{zi}后得到一个剩余的函数w即为Ωp上的调和函数,并且w在边界上光滑,从而得到式(4)
| $ u = g\left( z \right) + w $ | (4) |
式(4)中
| $ g\left( z \right) = \sum\limits_i {\left( {{\alpha _i} - 1} \right)\frac{\partial }{{\partial n}}\left( {\ln \left| {z - {z_i}} \right| - \ln \left| {z - z_i^*} \right|} \right)} $ |
且w满足边界条件
| $ \frac{{\partial w}}{{\partial n}} = - g\left( z \right) - X\left( s \right) - 2\pi r_{\rm{v}}^{ - 1}{{\rm{e}}^u} $ |
求解如式(5)的泛函φ(w)的最小值可以得到调和函数w。
| $ \begin{array}{*{20}{c}} {\phi \left( w \right) = \frac{1}{2}\iint_{{\mathit{\Omega }_{\text{p}}}} {{{\left\| {\nabla w} \right\|}^2}} + \int_{\partial {\mathit{\Omega }_{\text{p}}}} {\left( {g + X\left( s \right)} \right)w{\text{d}}s} + } \\ {2\pi \sum\limits_{v'} {\ln \int_{{C_{\text{v}}}} {\left| G \right|{{\text{e}}^w}{\text{d}}s,v' = 1,2,3 \cdots } } } \end{array} $ | (5) |
式中,Cv表示Ωa的内部边界,且
| $ G\left( z \right) = {\prod\limits_i {\left( {\frac{{z - {z_i}}}{{z - z_i^*}}} \right)} ^{\alpha - 1}} $ | (6) |
得到调和函数w后,求解Cauchy-Riemann方程
注意到G(z)是解析函数,则ln|G(z)|是从式(4)u中减去的奇异部分之和,因此f′(z)=exp(w+iwc)G(z)是解析函数,通过对f′(z)积分可以得到共形映射f(z)。
为了使调和函数w唯一,需要在外边界上选取两个点pi(i=1, 2(3)),从而得到限制条件式(7)
| $ \left\{ \begin{array}{l} \int_{{p_i}}^{{p_{i + 1}}} {\left| G \right|{{\rm{e}}^w}{\rm{d}}s = {a_i}} ,i = 1,2\left( 3 \right)\left( {{p_3} = {p_1}} \right)\\ \int_{{C_{{\rm{v1}}}}} {\left| G \right|{{\rm{e}}^w}} = \int_{{C_{{\rm{v2}}}}} {\left| G \right|{{\rm{e}}^w}} \end{array} \right. $ | (7) |
式(7)中ai为2个固定正数,令其满足a1+a2=2π,则式(7)可使映射f唯一,同时不影响目标网格的形状,更重要的是可以使内部边界的形状和大小变得相同。
1.2 数值求解通过有限元方法对公式(5)进行离散来寻找函数ϕ(w)的最小值。在Ωa区域打上网格点进行三角划分,并在每个尖角点部分进行加细处理。分别用V、E、F来表示节点、边和三角形的集合,并将未知函数w离散化为τ上的分段线性函数。
首先,将式(5)中的第一项离散为
| $ \;\;\;\;\;\;\iint_{{\mathit{\Omega }_{\text{p}}}} {{{\left\| {\nabla w} \right\|}^2}} = \sum\limits_H {\sum\limits_{k = 1}^3 {\frac{{\cot {\beta _k}}}{2}\left( {w\left( {{z_{k + 2}}} \right) - } \right.} } \\ {\left. {w\left( {{z_{k + 1}}} \right)} \right)^2} \\ $ | (8) |
式中H表示三角网格的个数。将w的离散值排成列向量w′,有
| $ {{\mathit{\boldsymbol{w'}}}^{\rm{T}}} = \left( {\mathit{\boldsymbol{w}}_{\rm{e}}^{\rm{T}},\mathit{\boldsymbol{w}}_{\rm{i}}^{\rm{T}}} \right) $ |
式中we是边界向量,wi是内部向量。所以式(8)等式右边可以写成矩阵表达式
| $ \mathit{\boldsymbol{A}} = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{{\rm{ee}}}}}&{{\mathit{\boldsymbol{A}}_{{\rm{ei}}}}}\\ {{\mathit{\boldsymbol{A}}_{{\rm{ei}}}}}&{{\mathit{\boldsymbol{A}}_{{\rm{ii}}}}} \end{array}} \right) $ |
式中Aee、Aii分别对应we和wi,Aei对应交叉部分。
其次,将式(5)中的第二项离散为
| $ \sum\limits_{e \in E} {\frac{{w\left( {s\left( e \right)} \right) + w\left( {t\left( e \right)} \right)}}{2}} \int_e {\left( {g + X\left( s \right)} \right){\rm{d}}s} $ | (9) |
式中e为三角网格的边。式(9)中g, X(s)可以分别离散为
| $ \left\{ \begin{array}{l} \frac{1}{2}\int_e {g{\rm{d}}s} = \frac{1}{2}\int_e {\left( {\frac{\partial }{{\partial n}}\ln \left| G \right|} \right){\rm{d}}s} = \\ \;\;\;\;\;\;\;\;\frac{1}{2}\int_e {\left( {\frac{\partial }{{\partial s}}{\rm{arg}} \ G } \right){\rm{d}}s} = \\ \;\;\;\;\;\;\;\;\frac{1}{2}\left[ {\arg \ G\left( {t\left( e \right)} \right) - \arg \ G\left( {s\left( e \right)} \right)} \right]\\ \frac{1}{2}\int_e {X\left( s \right){\rm{d}}s} = \frac{1}{2}\left( {{\rm{arctan}}\left( {y'\left( s \right)/x'\left( s \right)} \right)@\left( {t\left( e \right) - } \right.} \right.\\ \;\;\;\;\;\;\;\;\left. {{\rm{arctan}}\left( {y'\left( s \right)/x'\left( s \right)} \right)@s\left( e \right)} \right) \end{array} \right. $ | (10) |
式(10)中,@s(e)表示在s(e)点的值。值得注意的是,X(s)=
最后,将式(5)中第三项离散为
| $ 2\pi \sum\limits_{v'} {\ln l\left( {{C_{\rm{v}}}} \right)} ,v' = 1,2,3 \cdots $ | (11) |
式(11)中
| $ l\left( {{C_{\rm{v}}}} \right) = \sum\limits_{p \in V \cap {C_{\rm{v}}}} {\mu \left( p \right){{\rm{e}}^{\mathit{\boldsymbol{w'}}\left( p \right)}}} $ | (12) |
式(12)中
| $ \mu \left( p \right) = \left| {G\left( p \right)} \right|\left( {l\left( {{e_1}} \right) + l\left( {{e_2}} \right)} \right)/2 $ | (13) |
式(13)中,l(e1)、l(e2)分别表示p点两端的边界边的长度。
限制条件式(7)可以离散为如下形式
| $ \left\{ \begin{array}{l} \sum\limits_{p \in {{C'}_i}} {\mu \left( p \right){{\rm{e}}^{\mathit{\boldsymbol{w'}}\left( p \right)}}} = {a_i},i = 1,2\left( 3 \right)\\ l\left( {{C_{{{\rm{v}}_{\rm{1}}}}}} \right) = l\left( {{C_{{{\rm{v}}_2}}}} \right) \end{array} \right. $ | (14) |
式中C′i是外边界pi与pi+1之间的节点集合,且p3=p1。
综合公式(8)~(10)的离散过程,可得式(5)的离散形式
| $ \begin{array}{l} \;\;\;\;\;\;\phi \left( {\mathit{\boldsymbol{w'}}} \right) = \frac{1}{2}{{\mathit{\boldsymbol{w'}}}^{\rm{T}}}\mathit{\boldsymbol{Aw'}} + {\mathit{\boldsymbol{\lambda }}^{\rm{T}}}{\mathit{\boldsymbol{w}}_{\rm{e}}} + 2\pi \sum\limits_{v'} {\ln \left[ {\sum\limits_{p \in {C_{\rm{v}}}} {\mu \left( p \right)} } \right.} \\ \left. {{{\rm{e}}^{{\mathit{\boldsymbol{w}}_{\rm{e}}}\left( p \right)}}} \right] \end{array} $ | (15) |
固定we,则当wi=-Aii-1Aiewe时,ϕ(w′)有最小值。因此式(15)的最小值问题等价于式(16)取最小值
| $ \begin{array}{l} \;\;\;\;\;\;\phi \left( {{\mathit{\boldsymbol{w}}_{\rm{e}}}} \right) = \frac{1}{2}\mathit{\boldsymbol{w}}_{\rm{e}}^{\rm{T}}\mathit{\boldsymbol{A'}}{\mathit{\boldsymbol{w}}_{\rm{e}}} + {\mathit{\boldsymbol{\lambda }}^{\rm{T}}}{\mathit{\boldsymbol{w}}_{\rm{e}}} + 2\pi \sum\limits_{v'} {\ln \left[ {\sum\limits_{p \in {C_{\rm{v}}}} {\mu \left( p \right)} } \right.} \\ \left. {{{\rm{e}}^{{\mathit{\boldsymbol{w}}_{\rm{e}}}\left( p \right)}}} \right] \end{array} $ | (16) |
式中A′=Aee-AieTAii-1Aie。
求得式(16)在约束条件式(14)下的最小值we,进而可得到式(15)的最小值w′。
通过求解公式(17)的最小值可以得到w的共轭调和函数
| $ \begin{array}{l} \;\;\;\;\;{w^c} = \sum\limits_H {\sum\limits_{i = 1}^3 {\frac{{\cot {\beta _i}}}{2}{{\left( {w_{i + 2}^c - w_{i + 1}^c} \right)}^2} - \sum\limits_{i = 1}^3 {w_i^c} } } \\ \left( {{w_{i + 2}} - {w_{i - 1}}} \right) \end{array} $ | (17) |
因为f′(z)=exp(w+iwc)G(z)已知,所以通过求解式(18)可以得到
| $ f\left( z \right) = \mathop {\min }\limits_f {\iint {\left\| {\nabla f - f'} \right\|}^2}{\text{d}}x{\text{d}}y $ | (18) |
式(18)的离散过程如下。
首先,对于三角网格中顶点坐标为z1, z2, z3的三角形,令f′=(f′(z1)+f′(z2)+f′(z3))/3,从而得到期望三角形的3个顶点的坐标
| $ \left\{ \begin{array}{l} z_1^{\rm{e}} = 0\\ z_2^{\rm{e}} = \overline {f'}\left( {{z_2} - {z_1}} \right)\\ z_3^{\rm{e}} = \overline {f'}\left( {{z_3} - {z_1}} \right) \end{array} \right. $ | (19) |
将坐标分为实部和虚部(xie, yie)(i=1, 2(3))。
其次,该期望三角形对于式(18)离散后的实部和虚部的影响分别为
| $ \sum\limits_{i = 1}^3 {\frac{{\cot {\beta _i}}}{2}{{\left( {{x_{i + 2}} - {x_{i + 1}} - x_{i + 2}^{\rm{e}} + x_{i + 1}^{\rm{e}}} \right)}^2}} $ | (20) |
| $ \sum\limits_{i = 1}^3 {\frac{{\cot {\beta _i}}}{2}{{\left( {{y_{i + 2}} - {y_{i + 1}} - y_{i + 2}^{\rm{e}} + y_{i + 1}^{\rm{e}}} \right)}^2}} $ | (21) |
最后,采用最小二乘法对式(20)、(21)分别求最小值,得到最小值点{xi}、{yi},即得f(zk)=xk+iyk。
因为在式(17)的计算中,wc的值相差一个实常数,所以f(z)的值可以相差一个复常数。这说明求出映射后还可以作平移和旋转变换来保持共形性质。图 1即为数值计算结果的图示,可看出对不同的转角,映射后的圆界区域有较高的重合度。

|
图 1 流动截面区域到圆界区域的共形映射 Fig.1 Conformal mapping from the flow section area to the circle area |
选择一个热传导方程来验证共形映射算法的可行性。设热传导方程的求解区域是类似于图 1中的双螺杆挤出机截面的三连通区域,其中外边界不随时间变化,两个内边界绕各自中心旋转。热传导方程如下
| $ \left\{ \begin{array}{l} {u_t} = {u_{xx}} + {u_{yy}} + f\left( {x,y,t} \right),t > 0,\left( {x,y} \right) \in {D_{\rm{t}}}\\ u{|_{t = 0}} = {u_0}\left( {x,y} \right)\\ u{|_{{L_0}}} = {u_{\rm{e}}}\left( {x,y,t} \right)\\ u{|_{{L_1}\left( t \right)}} = {u_1}\left( {x,y,t} \right)\\ u{|_{{L_2}\left( t \right)}} = {u_2}\left( {x,y,t} \right) \end{array} \right. $ | (22) |
利用共形映射将求解区域Dt变为圆界区域,将自变量(x, y)变为(ξ, η),即得
| $ \left\{ \begin{array}{l} \xi = \xi \left( {x,y,t} \right)\\ \eta = \eta \left( {x,y,t} \right)\\ \theta = t \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = x\left( {\xi ,\eta ,\theta } \right)\\ y = y\left( {\xi ,\eta ,\theta } \right)\\ t = \theta \end{array} \right. $ | (23) |
假设此变换将Dt变为不随时间变化的区域Ω,边界L0、L1(t)、L2(t)分别变为
| $ \left\{ \begin{array}{l} {u_\theta } = \left( {\xi _x^2 + \xi _y^2} \right)\left( {{u_{\xi \xi }} + {u_{\eta \eta }}} \right) - {\xi _t}{u_\xi } - {\eta _t}{u_\eta } + \\ \;\;\;\;\;\;\;f\left( {x\left( {\xi ,\eta ,t} \right),y\left( {\xi ,\eta ,t} \right),t} \right),\theta > 0,\left( {\xi ,\eta } \right) \in \mathit{\Omega }\\ \mathit{u}{\mathit{|}_{\theta = 0}} = {u_0}\left( {x\left( {\xi ,\eta ,0} \right),y\left( {\xi ,\eta ,0} \right)} \right)\\ \mathit{u}{\mathit{|}_{{{\tilde L}_0}}} = {u_0}\left( {x\left( {\xi ,\eta ,t} \right),y\left( {\xi ,\eta ,t} \right),t} \right)\\ \mathit{u}{\mathit{|}_{{{\tilde L}_1}}} = {u_1}\left( {x\left( {\xi ,\eta ,t} \right),y\left( {\xi ,\eta ,t} \right),t} \right)\\ \mathit{u}{\mathit{|}_{{{\tilde L}_2}}} = {u_2}\left( {x\left( {\xi ,\eta ,t} \right),y\left( {\xi ,\eta ,t} \right),t} \right) \end{array} \right. $ | (24) |
式(24)中,螺杆转角θ>0, (ξ, η)∈Ω。式(24)可以通过有限元方法计算求解,共形映射和其逆映射的值以及相关导数值可以通过插值和变换之间的导数关系给出。
2.2 数值计算结果选取Dt的外边界为圆心在原点、半径等于r的圆周,其内边界L1(t)、L2(t)分别是椭圆,椭圆方程为
| $ \frac{{{{\left[ {\left( {x \mp c} \right)\cos \ \omega t + y \sin \ \omega t} \right]}^2}}}{{{a^2}}} + \frac{{{{\left[ {\left( {x \mp c} \right)\sin \ \omega t - y \cos \ \omega t} \right]}^2}}}{{{b^2}}} = 1 $ |
取r=2, a=0.6, b=0.8, c=0.8, ω=1,则定解问题式(22)变为
| $ \left\{ \begin{array}{l} {u_t} = {u_{xx}} + {u_{yy}} - 2,t > 0,\left( {x,y} \right) \in {D_t}\\ u{|_{t = 0}} = \sin \ x\cos \ y + {x^2}\\ u{|_{{L_0}}} = {{\rm{e}}^{ - 2t}}\sin \ x\cos \ y + {x^2}\\ u{|_{{L_1}\left( t \right)}}{\rm{ = }}{{\rm{e}}^{ - 2t}}\sin \ x\cos \ y + {x^2}\\ u{|_{{L_2}\left( t \right)}} = {{\rm{e}}^{ - 2t}}\sin \ x\cos \ y + {x^2} \end{array} \right. $ | (25) |
式(25)中,螺杆转动时间t>0, (x, y)∈Dt。
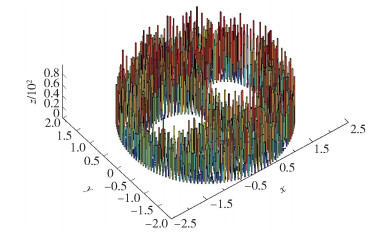
给定精确解u=e-2tsin xcos y+x2。取边界上初始网格长度0.08且均匀分布的三角网格,区域上约有1 700个网格点,在此网格上计算共形映射。数值解的求解过程为:首先对t从0~π/2进行离散,再对每个离散的t计算共形映射,然后利用对称性拓展得到π/2~π对应的离散t的共形映射,最后进行周期延拓,就可以得到所需的共形映射。将时间步长取为π/40,然后在映射网格上用有限元法求解式(25),得到t=2π时的数值解与精确解的绝对误差如图 2所示。
|
图 2 t=2π时数值解与精确解的绝对误差 Fig.2 Absolute errors of numerical solutions and exact solutions when t=2π |
通过比较数值解和精确解可知,其绝对误差在0.01范围内,表明本文算法是可行的。
3 结论(1) 用共形映射将双螺杆挤出机流体流动区域的截面变为圆界区域,可使求解区域不受转动的影响,将双螺杆挤出机流体流动区域进一步变换成截面为圆界区域的柱体区域,可以为双螺杆挤出机这种复杂流体运动的求解提供一种精确高效的方法。
(2) 利用本文方法对求解区域类似于双螺杆挤出机截面的三连通区域的热传导问题进行数值实验,得到的数值解与精确解误差较小,从而证明了本文方法的可行性和有效性。
| [1] |
ZHANG X M, FENG L F, CHEN W X, et al. Numerical simulation and experimental validation of mixing performance of kneading discs in a twin screw extruder[J]. Polymer Engineering & Science, 2010, 49(9): 1772-1783. |
| [2] |
邱国庆, 李翱, 毕超, 等. 同向双螺杆挤出机混合型螺杆头均温效果三维非等温数值模拟[J]. 塑料, 2010, 39(5): 71-75. QIU G Q, LI A, BI C, et al. 3-D non-isothermal numerical simulation of the effect of temperature mixing in mixing screw head of co-rotating twin-screw extruder[J]. Plastics, 2010, 39(5): 71-75. (in Chinese) DOI:10.3969/j.issn.1002-1396.2010.05.019 |
| [3] |
PENG J, CHEN J N. Numerical simulations of polymer melt conveying in co-rotating twin screw extruder[J]. Journal of Beijing Institute of Technology(English Edition), 2002, 11(2): 189-192. |
| [4] |
伍继梅.单螺杆挤出机三维数值模拟的研究[D].北京: 北京化工大学, 2014. WU J M. The study on the 3-dimensional numerical simulation of single screw extuder[D]. Beijing: Beijing University of Chemical Technology, 2014.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10010-1015581194.htm |
| [5] |
王国娟.单螺杆挤出机三维模型几何变换算法的研究[D].北京: 北京化工大学, 2016. WANG G J. The study on the geometric transformation algorithm of single screw extuder in the 3-dimensional space[D]. Beijing: Beijing University of Chemical Technology, 2016.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10010-1016322290.htm |
| [6] |
黄硕, 黄晋阳. 用区域变换计算单螺杆挤出机流动区域上的三维泊松方程数值解法[J]. 北京化工大学学报(自然科学版), 2017, 44(5): 118-122. HUANG S, HUANG J Y. Using area transformation to solve the 3D Poisson equation in the flow area of a single screw extruder[J]. Journal of Beijing University of Chemical Technology(Natural Science), 2017, 44(5): 118-122. (in Chinese) |
| [7] |
WEGMANN R. Fast conformal mapping of multiply connected regions[J]. Journal of Computational and Applied Mathematics, 2001, 130: 119-138. DOI:10.1016/S0377-0427(99)00387-8 |
| [8] |
MURID A H M, HU L N. Numerical conformal mapping of bounded multiply connected regions by an integral equation method[J]. Int J Contemp Math Sciences, 2009, 4(23): 1121-1147. |
| [9] |
LUO W, DAI J F, GU X F, et al. Numerical conformal mapping of multiply connected domains to regions with circular boundaries[J]. Journal of Computational & Applied Mathematics, 2010, 233(11): 2940-2947. |








