2. 北京化工大学 理学院, 北京 100029
2. Faculty of Science, Beijing University of Chemical Technology, Beijing 100029, China
Stewart平台是一个最基本的空间并联机构,1956年由Gough为测试轮胎性能而设计[1],1965年由Stewart[2]正式在论文中提出。它由1个定平台(基座)、1个动平台以及连接两个平台间可伸展的6条腿组成,可应用于多个领域,如机器人、数控机床、天文望远镜等[3]。由于并联机构互补于串联机构,具有承载能力高、精度高、实时控制等特点,Stewart平台已经成为机构学研究领域和智能装备制造领域中研究的热点。
Stewart平台的位置正解问题是指给定基座和动平台间6条腿的杆长,确定动平台的位姿。研究位置正解的目的在于为并联机构的设计提供必要的依据。例如,在解决如何用最小的机构尺寸获得必需的工作空间、如何避开机构运动的奇异位形等问题时,都要求获得并联机构的位置正解[4]。Stewart平台位置正解的求解十分困难,作为21世纪100个交叉科学难题之一[3],到目前为止还未彻底解决。解决该问题较为常用的方法是数值法[3]和解析法[4]。解析法求解过程虽然较为复杂,但是不需要设置初始值,而且可以求得全部的解析解,可为并联机构的设计提供强有力的支持。
在并联机构研究的初期,以空间六自由度并联机构为主。随着研究的深入,研究人员发现少自由度并联机构与六自由度并联机构相比,具有结构简单、易于控制且制造成本低的优点。少自由度并联机构尤其是三自由度并联机构在包装、数控精密绣花机以及医疗手术等领域显现出十分广阔的发展前景[5],得到了科学界和产业界的重视。平面并联机构中的平面Stewart平台就是一个三自由度并联机构,从结构上看,它包括1个定平台(基座)、1个动平台以及连接两个平台间可伸展的3条腿。
文献[6]证明了平面Stewart平台的位置正解的个数最多为6个。文献[7]根据除去驱动副后各支链形成的不同形式把平面并联机构分为RRR、PRR、RPR、RRP、PPR、PRP、RPP共7类(其中R表示转动副,P表示移动副)。文献[8]应用吴消元法[9]研究了3-RPR平面并联机构的位置正解,得到了包含一元六次方程的闭形解。
为了设计更易操作的并联机构,文献[10]从几何约束求解的角度提出了空间广义Stewart平台(generalized Stewart platform, GSP)的概念,即定平台(基座)和动平台均为刚体,基座和动平台由6个点、线、面间的角度约束与距离约束连接。根据添加约束的不同,可以将空间广义Stewart平台分为3 850种。在不考虑平面副的条件下,文献[11]根据两个优化准则,从3 850种GSPs中选出195种非对称类型并联机构进行研究。文献[12]对空间广义Stewart平台的位置正解求解策略作了详细研究。文献[13-14]提出了平面广义Stewart平台的概念,并根据添加约束的不同,把平面广义Stewart平台位置正解问题分为16种子情况,给出了每种情形的闭形解及取得实数解的参数条件。
本文在文献[12-14]工作的基础上,根据基座和平台间的约束及平台上几何体之间的约束关系生成约束图,对其进行完备化,生成构造序列,降低求解规模;并对平面广义Stewart平台位置正解进行了基于MapleSim软件的仿真,用实例验证了方法的有效性。
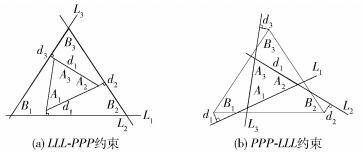
1 基本概念 1.1 平面广义Stewart平台平面广义Stewart平台是由1个位置固定的刚体(称为基座)、1个移动的刚体(称为动平台或平台),以及连接基座和平台之间的3对点/线、点/点或线/线间的距离或角度约束组成。其中,L-P表示基座上直线L和平台上点P之间的约束;P1-P2表示基座上点P1和平台上点P2之间的约束;L1-L2表示基座上直线L1和平台上直线L2之间的约束。例如,LLL-PPP表示基座上3条直线到平台上3个点的距离;PPP-LLL表示基座上3个点到平台上3条边的距离,如图 1所示。
|
图 1 LLL-PPP约束与PPP-LLL约束 Fig.1 Constraints of LLL-PPP and PPP-LLL |
平面广义Stewart平台的约束类型分为两类:2个距离约束和1个角度约束(DDA),以及3个距离约束(DDD)。其中,DDA包含6种子类型,即LLL-LPP、LLP-LPL、LLP-LPP、LPP-LLL、LPP-LLP、LPP-LPP;DDD包含10种子类型,即PPP-LLL、LLL-PPP、LLP-PPL、LLP-PPP、LPP-PLL、PPP-LLP、LPP-PLP、LPP-PPP、PPP-LPP、PPP-PPP[14]。其中的PPP-PPP型平面广义Stewart平台就是平面Stewart平台。
1.2 自由度与约束度自由度(degree of freedom, DOF)是指在几何空间中没有受到约束的几何元素、几何实体或者机械系统的位置所需要的最少广义坐标数(即所需要的自由变量的个数)。例如,平面上点和线的自由度为2,刚体的自由度为3,由1个旋转自由度和2个平移自由度组成。约束度(degree of constraint, DOC)表示距离或角度约束所对应的标量方程的个数。用pi、li分别表示点和线,距离约束或角度约束的约束度如下:
(1) ANG(l1, l2)表示直线l1和l2之间的角度约束,其约束度为1;
(2) DIS(l1, l2)表示互相平行的两条直线l1和l2之间的距离约束,其约束度为2;
(3) DIS(p1, l1)表示点p1和直线l1之间的距离约束,其约束度为1;
(4) DIS(p1, p2)表示点p1和点p2之间的距离约束,若点p1和p2重合,其约束度为2;否则,其约束度为1。
1.3 约束图平面广义Stewart平台的位置正解问题可用二部图G=(V, C, E)表示,称之为约束图,其中:
(1) 在约束图G中,V表示外部约束所包含的几何体的集合,V中几何体的个数为2或3;
(2) C表示距离或角度约束构成的顶点集,C中的约束分为外部约束和内部约束,内部约束是指平台上几何体之间的约束,外部约束是指基座和平台上几何体之间的约束;
(3) E={(c, v)|v∈V, c∈C},E中的元素为c到v的边,其方向为v到c,其中V中的顶点v的外部约束度为1或2;
(4) 对于任意顶点v∈V,若指向顶点v的边的约束度之和等于该点的自由度,即称该点是饱和的;小于该点则称为不饱和的。
2 平面广义Stewart平台位置正解约束图的分类根据平面广义Stewart平台的基座和平台间添加的外部约束所包含的点的个数,生成位置正解对应的约束图,对其采用欠约束系统完整约束完备化方法[15],生成构造序列。根据构造序列的类型,可将平面广义Stewart平台位置正解分为两类,即有循环约束问题和无循环约束问题。其中,无循环约束问题的约束图包含两个几何体,可以逐点顺序求解;有循环约束问题的约束图包含3个几何体,需要几个未知数一同求解,需同时求解的方程组规模相对较大,复杂度也较高。
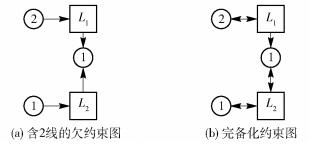
2.1 约束图中包含两个几何体的情形在图 2中,圆圈表示约束,圆圈内的数字表示对应的距离约束或角度约束的约束度之和,方块表示平台上的点或线。当约束图中有两个几何体时,属于无循环约束问题。根据几何体的类型共有3种子情况,即2个不重合的点、2条相交的直线或者1个点1条线。
|
图 2 包含两个几何体的约束图及其完整约束完备化图 Fig.2 Constraint graph consisting of two geometric vertices and the well-constrained completion graph |
例如,图 2(a)所示的约束图中L1和L2均为不饱和的(L1和L2相交)。对图 2(a)进行完整约束完备化后,得到的约束图如图 2(b)所示,图中的L1和L2均为饱和的,可以得到构造序列为{{L1}, {L2}},即先确定L1的位置,再确定L2的位置,由此确定平台位置。此种情况即为可逐点求解的类型,2个点、1点1线均可类似逐点构造。
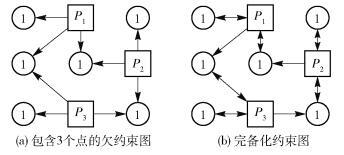
2.2 约束图中包含3个几何体的情形当约束图中有3个几何体时,属于有循环约束问题。每个外部约束的约束度为1,根据几何体的类型共有4种子情况,即3个点、3条线、2点1线和1点2线。3点约束情况如图 3所示。
|
图 3 包含3个几何体的约束图及其完整约束完备化图 Fig.3 Constraint graph consisting of three geometric vertices and the well-constrained completion graph |
例如,图 3(a)所示的约束图中包含3个外部约束,P1, P2, P3均为不饱和的。对图 3(a)采用完整约束完备化方法后,约束图如图 3(b)所示,该图中3个点均为饱和的,构造序列为{{P1, P2, P3}}。因此,方程组只能同时求解,此种情况即为不可逐点求解的类型。此外,3条线、2点1线和1点2线均可类似构造。
3 平面广义Stewart平台位置正解求解策略与仿真 3.1 位置正解求解策略平面广义Stewart平台通过加入约束条件,可将位置正解问题转化为非线性方程组求解问题,即几何约束求解问题,其求解策略如下。
(1) 根据约束条件将平面广义Stewart平台的位置正解问题转化为约束图。
(2) 对约束图进行完整约束完备化,将位置正解问题分为两类:若约束图中包含两个几何体,则为无循环约束问题;若包含3个几何体,则为有循环约束问题。
(3) 对于无循环约束问题,需要依照构造序列逐点求解;对于有循环约束问题,则不可逐点构造,需要同时求解。
(4) 在解决非线性方程组时,用吴消元法对需同时求解的代数方程组进行消元化简,得到闭形解。
3.2 仿真通用计算机代数系统Maple具有强大的符号计算能力,MapleSim软件是基于计算机代数系统Maple,建立在符号与数值混合计算技术基础上的软件,可以实现系统的建模、分析和仿真。Maple和MapleSim软件可以有效地处理平面广义Stewart平台位置正解问题在求解与仿真过程中所涉及的关于吴消元法的符号计算问题。文献[16]采用MapleSim软件研究了Stewart平台的运动学逆解问题。
本文研究的平面广义Stewart平台位置正解仿真问题中的基座为正三角形B1B2B3,平台为正三角形A1A2A3。参考文献[16]中的方法,搭建了基于Maple和MapleSim软件的平面广义Stewart平台位置正解的仿真平台,具体流程如下。
(1) 搭建分支并设置分支参数。在MapleSim的元件库中找到各分支所需元件,按照虎克铰移动副、球副的顺序连线,设置分支的各项参数。
(2) 创建子系统项并配置子系统的各项参数,复制到3个分支上。动平台用变量A表示,固定平台用变量B表示,X, Y, Z分别表示该方向的分量(平面中Z=0)。进入参数块输入XA1、YA1、ZA1、XB1、YB1、ZB1参数名称,作为平面广义Stewart平台第一分支P1的坐标点,设置参数块配置模型参数,且复制P2、P3作为平面广义Stewart平台第二、三分支。
(3) 搭建平台,连接每个分支,并配置平台的模型参数。
(4) 在MapleSim软件的分析模板中添加自定义模板,创建新的Linkmodel进入Maple环境,建立Maple和MapleSim之间的连接。
(5) 在Maple中输入平台和基座间的约束,生成代数方程组,并用吴消元法进行消元并求解。
(6) 将求得的解赋值给平台末端,运行生成模型。
4 实例验证 4.1 参数设置设平台为正三角形A1A2A3,位姿确定时3条边所在直线分别为A1A2、A2A3、A1A3,3条边对应的直线方程组如式(1)所示
| {A1A2:k1x−y+b1=0A2A3:k2x−y+b2=0A1A3:k3x−y+b3=0 | (1) |
根据所给的3个约束条件确定多元非线性方程组,该问题化为求解多元非线性代数方程组问题。将参数带入式(1)中,得到旋转矩阵R=(rij)2×2和平移矩阵T=(t1, t2)T,其中,RRT=RTR=I,det(R)=1,r22=r11,r12=-r21。
设基座对应的正三角形B1B2B3边长为b,平台对应的正三角形A1A2A3边长为a。顶点A1,A2,A3在局部坐标系中的坐标为A1:(0,0),A2:(a,0),A3:
本文对16种不同情况的平面广义Stewart平台进行研究,给出了对应的位置正解及基于MapleSim的位置正解仿真。
由于文章篇幅限制,本节仅以DDA和DDD中的两个实例为例,说明具体求解及仿真方法,其余的情形均可按此方法求解。
4.2 DDA约束以DDA中的LPL-LPP类型为例。设点A1在全局坐标系中的坐标为(x, y),基座与平台间的角度约束为直线A1A2与直线B1B2间的夹角θ,距离约束为平台上点A1到基座上点B1的距离d1(d1>0),以及平台上点A1到基座上直线B1B2的距离d2,对应多元多项式方程组(2)。其中k1=tanθ表示直线A1A2在全局坐标系中的斜率,未知量为y,x,b1。
| {d1=x2+y2d2=|y|y=k1x+b1 | (2) |
由给定的3个约束可知,该问题为可逐点求解问题,分配给点A1和直线A1A2的约束度之和分别为2和1。可以根据点A1和点B1间的距离、点A1到直线B1B2的距离先确定出A1的位置,再由DIS(A1, A2)和角度θ确定A2的位置。
当方程组(2)经吴消元法直接求解后,得到特征列(式(3)),其中D2=±d2。
| {y−D2=0x2−d21+D22=0b1+k1x−D2=0 | (3) |
由方程组(3)可知,方程组解的个数取决于第2个关于x的一元二次方程。因此方程组(3)解的个数为:①d1>d2时,有4组解;②d1=d2时,有2组解;③d1 < d2时,无解。
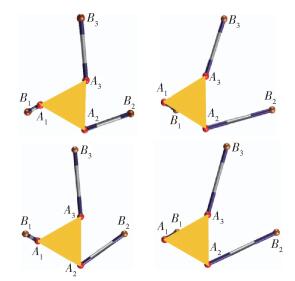
令
|
图 4 LPL-LPP型平面广义Stewart平台位置正解仿真 Fig.4 Simulation of direct kinematics for the LPL-LPP planar generalized Stewart platform |
以DDD中的LLP-PPP类型为例。设距离约束如下:平台上点A1到基座上点B1的距离为d1(d1>0),平台上点A3到基座上直线B1B2的距离为d2,平台上点A2到基座上直线B1B2的距离为d3,对应多元多项式方程组(4),未知量为t1,t2,r11,r21。
| {d21=t21+t22d2=|a2(r21+√3r11)+t2|d3=|ar21+t2|r211+r221=1 | (4) |
给定3个距离约束条件后,约束图包含3个几何体,必须同时求解,对应的约束图为图 3(b)。式(5)是方程组(4)通过吴消元法得到的特征列,其中D2=±d2,D3=±d3。
| {4t22−4(D2+D3)t2−4D2D3+4D22+4D23−3a2=04t21+4(D2+D3)t2−4d21+4D2D3−4D22−4D23+3a2=0ar21−D3+t2=03ar11+√3t2−2√3D2+√3D3=0 | (5) |
方程组(5)中第3个方程关于t2的解为
令
|
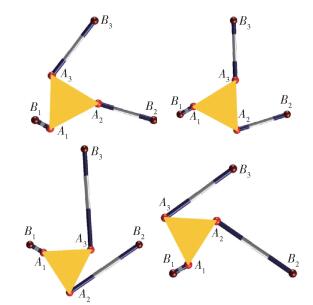
图 5 LLP-PPP型平面广义Stewart平台位置正解仿真 Fig.5 Simulation of direct kinematics for the LLP-PPP planar generalized Stewart platform |
本文从几何约束求解的角度出发,结合图论分析和符号计算的方法,研究了平面广义Stewart平台的位置正解求解策略及仿真问题,对实例进行验证的结果表明了本文方法的有效性。
平面广义Stewart平台是三自由度并联机构Stewart平台的推广形式,针对其展开研究对并联机构的设计及其相关应用领域的发展具有普遍意义。今后计划在本文工作的基础上,进一步对平面广义Stewart平台的工作空间、奇异位形等问题展开研究。
| [1] |
廖启征. 连杆机构运动学几何代数求解综述[J]. 北京邮电大学学报, 2010, 33(4): 1-11. LIAO Q Z. Geometry algebra method for solving the kinematics of linkage mechanisms[J]. Journal of Beijing University of Posts and Telecommunications, 2010, 33(4): 1-11. (in Chinese) |
| [2] |
STEWART D. A platform with six degrees of freedom[J]. Proceedings of the Institution of Mechanical Engineers, 1965, 180(1): 371-386. DOI:10.1243/PIME_PROC_1965_180_029_02 |
| [3] |
韩方元. 并联机器人运动学正解新算法及工作空间本体研究[D]. 长春: 吉林大学, 2011. HAN F Y. The research on novel forward kinematics numerical algorithm and workspace ontology for parallel robot[D]. Changchun: Jilin University, 2011. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10183-1012257726.htm |
| [4] |
黄昔光, 黄旭. 利用共形几何代数的平面并联机构位置正解求解方法[J]. 西安交通大学学报, 2018, 52(3): 76-82. HUANG X G, HUANG X. Direct kinematics of planar parallel mechanisms based on conformal geometric algebra[J]. Journal of Xi'an Jiaotong University, 2018, 52(3): 76-82. (in Chinese) |
| [5] |
董倩文. 3-PRP平面并联机构的运动与刚度性研究[D]. 太原: 中北大学, 2015. DONG Q W. Research on kinematics and stiffness characteristics of 3-PRP planar parallel mechanism[D]. Taiyuan: North University of China, 2015. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D640611 |
| [6] |
PENNOCK G R, KASSNER D J. Kinematic analysis of a planar eight-bar linkage:application to a platform-type robot[J]. Journal of Mechanical Design, 1992, 114(1): 87-95. DOI:10.1115/1.2916930 |
| [7] |
MERLET J P. Direct kinematics of planar parallel manipulators[C]//Proceedings of the 1996 IEEE International Conference on Robotics and Automation. Minneapolis, 1996: 3744-3749.
|
| [8] |
刘惠林, 张同庄. 3-RPR平面并联机构正解的吴方法[J]. 北京理工大学学报, 2000, 20(5): 565-569. LIU H L, ZHANG T Z. Forward solutions of the 3-RPR planar parallel mechanism with Wu's method[J]. Transaction of Beijing Institute of Technology, 2000, 20(5): 565-569. (in Chinese) |
| [9] |
吴文俊. 几何定理机器证明的基本原理:初等几何部分[M]. 北京: 科学出版社, 1984. WU W J. The basic principles of geometric theorem proving:elementary geometry[M]. Beijing: Science Press, 1984. (in Chinese) |
| [10] |
GAO X S, LEI D L, LIAO Q Z, et al. Generalized Stewart-Gough platforms and their direct kinematics[J]. IEEE Transactions on Robotics, 2005, 21(2): 141-151. DOI:10.1109/TRO.2004.835456 |
| [11] |
TOZ M, KUCUK S. Parallel manipulator software tool for design, analysis, and simulation of 195 GSP mechanisms[J]. Computer Applications in Engineering Education, 2015, 23(6): 931-946. DOI:10.1002/cae.v23.6 |
| [12] |
ZHANG G F, ZHANG J W, ZHAO L N. Strategies on direct kinematics to generalized Stewart platforms[C]//2016 International Conference on Electrical Engineering and Automation. Xiamen, 2016: 451-456.
|
| [13] |
ZHANG G F, GAO X S. Planar generalized Stewart platforms and their direct kinematics[M]//HONG H, WANG D. Automated deduction in geometry. Berlin: Spinger, 2006: 198-211.
|
| [14] |
ZHANG G F. Classification of direct kinematics to planar generalized Stewart platforms[J]. Computational Geometry:Theory and Applications, 2012, 45(8): 458-473. DOI:10.1016/j.comgeo.2010.06.007 |
| [15] |
ZHANG G F, GAO X S. Well-constrained completion and decomposition for under-constrained geometric constraint problems[J]. International Journal of Computational Geometry & Applications, 2006, 16(5/6): 461-478. |
| [16] |
MapleSim_符号方式求解Stewart平台的逆运动学问题[EB/OL]. (2017-11-01). http://www.cybernet.sh.cn/solution/s19.html. MapleSim_solving inverse kinematics to Stewart platform with symbolic method[EB/OL]. (2017-11-01). http://www.cybernet.sh.cn/solution/s19.html. (in Chinese) |









