2. 北京化工大学 高分子材料加工装备教育部工程研究中心, 北京 100029
2. Engineering Research Center of Polymer Processing Equipment, Ministry of Education, Beijing University of Chemical Technology, Beijing 100029, China
微热压印成型技术是聚合物微纳制造领域最重要的技术之一,而探寻聚合物在不同条件下的黏弹性规律是提高微热压印过程效率和降低微热压印成本的重要基础。相对于宏观尺度,聚合物在微纳米数量级上的材料性质更取决于原子和分子之间的相互作用力,而分子动力学模拟为在微观尺度上的建模提供了独特的方法[1]。Hossain和Tschopp等[2]对无定形聚乙烯在单轴压缩过程中的应力应变行为进行了分子动力学分析;此外,许多学者利用分子动力学模拟的方法对纳米压印过程中聚合物分子链的运动状况、基底的变形、压印和脱模过程、微结构制品的复制率以及缺陷的影响、聚合物的界面行为等进行了研究[3-8]。
作者所在团队经过一系列实验与理论研究,提出聚合物类固态等温微热压印方法,大大缩短了压印周期[9-11]。其中,类固态是指被压印聚合物处于玻璃化转变温度Tg(无定形聚合物)附近或结晶熔点Tm(结晶型聚合物)附近的非流动状态,等温是指模具在整个热压印周期保持恒温。这种状态下聚合物处于玻璃态向橡胶态转化的过程中,会“软化”并具备弹塑性。聚合物快速、小形变的应力应变关系非常复杂,同时,由于加工温度远低于流动温度Tf,内应力在保压和脱模过程中如果没有得到充分松弛则直接影响微纳结构的几何稳定性,然而相关的松弛规律的研究却很少。为此,本文基于分子动力学模拟方法,从能量、分子密度、分子尺寸变化、速度分布以及速度相关函数等角度,对类固态微热压印过程中聚合物松弛规律进行了分析。
1 模型构建与模拟参数的选择本文采用Materials Studio8.0进行分子动力学模拟,选取常被用于类固态微压印的典型无定型聚合物聚甲基丙烯酸甲酯(PMMA),以镍为刚性模具基底与PMMA基片组合[12]。体系内所有有关的计算过程均采用COMPASS分子力场来实现,它在原有计算分子键参数方法的基础上采用液态分子动力学作为参数化的实验标准,因而可以得到关于凝聚态材料更加精准的计算结果[13-14]。
1.1 模具镍层体系的构建根据Kittel的固体物理学[15],晶体轴长为0.352 nm,晶体轴角为90°。对镍晶胞沿着(1 0 0)面进行面切割,设定镍层高度为2 nm,截取后的单个晶胞如图 1所示。然后设定扩展后晶体轴长为2.0 nm,晶体轴角为90°,以此构造超胞来增大表面积,达到阵列效果。并对超胞体系进行能量最小化处理和固定处理,构造出1.0 nm×1.0 nm的纳米凹槽结构,如图 2所示。

|
图 1 镍晶胞的表面构建图 Fig.1 Surface construction of the nickel cell |

|
图 2 带纳米型腔的镍超胞结构 Fig.2 Nickel super cell structure with a nanometer cavity |
优化处理PMMA氢原子位置,得到单链PMMA聚合分子和体系优化后的低能结构,并将其引入无定形单胞,设定密度为1.19 g/cm3,如图 3所示。对其进行能量最小化和5次循环退火处理,除去内应力,使无定形聚合物体系达到相对平衡状态,提高模拟的准确性。退火初始温度为298 K,退火温度为500 K。然后使用分层建模工具将PMMA无定形聚合体系添加到镍层表面,为避免高度方面受三维周期性边界条件的影响,在聚合物层的上方添加真空层,设置真空层厚度为3.0 nm,模拟盒子尺寸为3 nm×3 nm×10 nm。构建完成的片层界面模型如图 4所示。
|
图 3 PMMA无定形聚合体系的构建 Fig.3 Construction of the PMMA amorphous polymerization system |

|
图 4 片层界面模型的构建 Fig.4 Construction of the layer interface model |
此外,对于静电相互作用力使用Ewald法进行计算,对于范德华力利用Atom based方法进行计算。计算步长设置为1fs。对于聚合物分子链段的计算是基于弹簧珠子模型进行的,其中包括键势能Φb(式(1))、角势能Φa(式(2))、扭转势能Φt(式(3))和Lennard Jones势能ΦLJ方程(式(4))[16-19]。其中Lennard Jones势能方程作用于不同的PMMA链段之间以及模具镍层和聚合物基材之间。当不同种类的联合原子发生相互作用时,Lennard Jones势能方程中的各个参数依据Lorentz-Berthelot混合规则进行计算求解。
| ${\mathit{\Phi }_{\rm{b}}} = \frac{1}{2}{K_{\rm{b}}}{({l_{ij}} - {l_0})^2} $ | (1) |
| $ {\mathit{\Phi }_{\rm{a}}} = \frac{1}{2}{K_{\rm{a}}}{({\theta _{ijk}} - {\theta _0})^2} $ | (2) |
| $ {\mathit{\Phi }_{\rm{t}}} = \sum\limits_{m = 0}^3 {{a_m}{{[{\rm{cos}}({\phi _{ijkl}})]}^m}} $ | (3) |
| $ {\mathit{\Phi }_{{\rm{LJ}}}} = 4{\varepsilon _{ij}}\left[{{{\left( {\frac{{{\sigma _{ij}}}}{{{r_{ij}}}}} \right)}^{12}}-{{\left( {\frac{{{\sigma _{ij}}}}{{{r_{ij}}}}} \right)}^6}} \right] $ | (4) |
其中,lij为键长,l0为平衡键长,Ka、Kb、am、εij为能量常数,θijk为弯曲角,θ0为平衡弯曲角,ϕijkl为扭转角,σij为比例常数(σij与εij的值取决于原子种类),rij为两个相互作用原子之间的间距。
1.3 模拟参数的选择聚合物在热压填充阶段压力恒定,假定系统处于准平衡的状态。选取等温等压(NPT)系综对热压的填充过程进行模拟,设定20000步,温度403.15 K,压强30.0 MPa,利用Pamnello-Rahman法控制体系压强,分析体系能量与纳米型腔内PMMA平均密度随时间的变化情况。
在保压松弛阶段,讨论模具镍层的表面和PMMA无定形聚合体系之间的非键作用,探究温度的变化对非键作用的影响,分析聚合物对纳米型腔的填充能力的强弱以及脱模过程的难易程度。相互作用能作为其体现形式,公式如下
| $ {E_{\rm{i}}} = {E_{\rm{t}}} - ({E_{\rm{n}}} + {E_{\rm{p}}}) $ | (5) |
其中,Ei为相互作用能;Et为模具镍层和PMMA无定形聚合体系的总能量;En为模型去除PMMA无定形聚合体系后模具镍层表面所具有的能量;Ep为模型除去模具镍层后PMMA无定形聚合体系所具有的总能量。
在应力松弛过程中,分子链产生相对滑移,逐渐恢复其蜷曲的原状,内应力逐渐消除,与之相平衡的外力逐渐衰减,以维持恒定的应变。均方回转半径Rg2是常用来表征聚合物分子尺寸的物理量,因此,为了体现保压阶段中PMMA无定形聚合体系所发生的应力松弛现象,选取均方回转半径这一构象统计规律表征PMMA分子链的平均尺寸随温度改变而变化的情况。同时,研究模具镍层微结构内的PMMA分子链的运动情况以及速度分布,并将速度自相关系数(即松弛过程速度与模拟初期速度的相关程度)随时间的变化情况作为宏观上PMMA片材在保压阶段所发生应力松弛现象的微观反映。另外,由于聚合物分子的运动具有温度依赖性,研究了温度发生变化时模具镍层型腔内PMMA分子链均方回转半径的平均值,以及平动速度自相关系数随时间的变化情况。
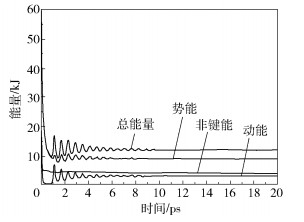
2 模拟结果与分析 2.1 热压填充过程的分子动力学在填充的过程中,PMMA的高分子链段在外界压力的影响下不断地克服链段间的相互作用力,逐步将纳米凹槽填充完全,如图 5所示。在整个热压填充模拟过程中体系的能量随时间的变化情况如图 6所示,可以看出整体热压填充模拟到9.6 ps时,体系的总能量、势能、非键能和动能都趋向于稳定。

|
图 5 模拟热压填充过程 Fig.5 Simulation of the hot embossing process |
|
图 6 体系能量随时间的变化 Fig.6 Variation of the system energy with time |
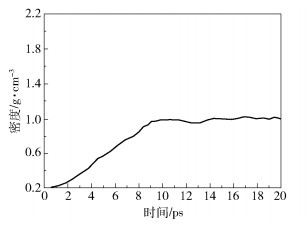
图 7为纳米型腔内PMMA无定形聚合体系的平均密度值随时间的变化关系。纳米型腔内PMMA的平均密度值随时间逐渐升高,在9.6 ps时趋于稳定,与整个体系进入较稳定状态同步。说明随着热压填充模拟体系的逐步稳定,PMMA分子链段的运动也由活跃趋于平稳,最终在纳米型腔内达到较稳定的结构,为后续PMMA无定形聚合体系在保压过程中松弛规律的模拟构建了合理的基础数据模型。
|
图 7 纳米型腔内PMMA平均密度随时间的变化 Fig.7 Variation of the mean density of PMMA in the nano-cavity with time |
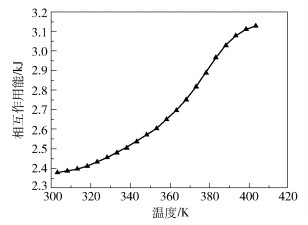
经计算,模具镍层表面和PMMA无定形聚合体系之间的相互作用能随温度的变化曲线如图 8所示。
|
图 8 镍层表面和PMMA无定形聚合体系之间相互作用能随温度的变化 Fig.8 Variation of the interaction energy between the surface of the nickel layer and the PMMA amorphous polymerization system with temperature |
图 8表明,温度的变化对相互作用能的影响非常大,随着温度升高,相互作用能逐渐增加;当温度升至PMMA的玻璃化转变温度(378.15 K)附近时,相互作用能变化尤为剧烈,增长幅度达到最大值;当温度超过378.15 K时,相互作用能增加到3000 J,此后增长速度逐渐变慢。
相互作用能的大小体现了PMMA分子链同镍原子层之间非键作用的强弱,当相互作用能较大时,PMMA分子链同镍原子层之间更容易形成稳定的非键合相互作用;而当相互作用能较小时,非键作用更易于被打破。因此在不同阶段对不同温度的选取,决定着聚合物对纳米型腔的填充能力的强弱以及脱模过程的难易程度。对于不同聚合物材料不同的微纳结构具有相异的成形要求时,应当在考虑聚合物同模具金属层之间相互作用能的基础上,适当选取加工过程不同阶段的温度。
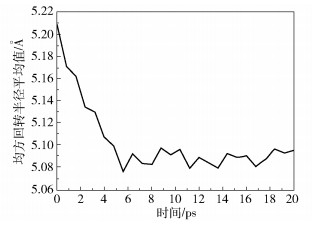
2.2.2 保压松弛过程中聚合物高分子链均方回转半径的变化情况当保压松弛阶段的温度为403.15 K时,对处于模具镍层型腔内的所有PMMA分子链的均方回转半径取平均值,得到在该温度下模具镍层的微结构内PMMA分子链均方回转半径的平均值随时间的变化情况如图 9所示。
|
图 9 模具镍层型腔内PMMA分子链均方回转半径的平均值随时间的变化 Fig.9 Variation of the average mean square radius of gyration of PMMA molecular chains in the cavity of the mold nickel layer with time |
当温度为403.15 K时,随着时间增加,平均值逐渐减小,并且减小的速度逐渐变缓,说明处于纳米型腔内的PMMA分子链在经历了填充阶段外力作用下充分伸展的形变过程之后,其链段运动逐渐减弱。受自身长链结构以及PMMA分子链中碳-碳单键内旋转的影响,PMMA的分子链重新发生蜷曲作用,直至达到该温度下熵的最大值。应力松弛过程是在外力作用下聚合物高分子链自身产生的缓慢构象重排和分子链的滑移的过程,高分子链自身的蜷曲作用以及速度的变化共同影响着聚合物应力松弛的过程。均方回转半径作为PMMA分子链尺寸最直接的表征参数,其值逐渐减小并趋于稳定反映了在保压阶段聚合物分子链的形态特征随时间的变化情况。
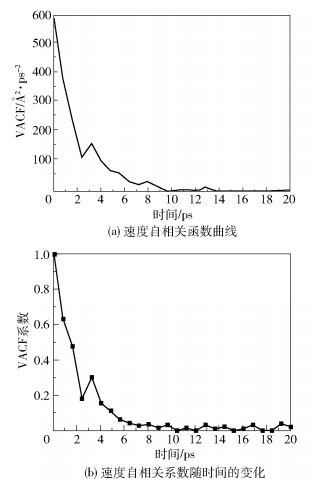
2.2.3 聚合物高分子链的速度分布以及速度自相关函数的变化情况当温度为403.15 K时,得到模具镍层纳米型腔内垂直于界面方向的PMMA分子链的速度自相关函数(VACF),对其进行归一化处理,得到其平动速度的自相关系数(VACF系数)随时间的变化情况,如图 10所示。
|
图 10 模具镍层型腔内PMMA分子链速度自相关函数与自相关系数随时间变化曲线 Fig.10 Variation of the velocity autocorrelation function curve and autocorrelation coefficient of PMMA molecular chains in the cavity of the mold nickel layer with time |
从图 10可以看出,当温度为403.15 K时,纳米型腔内PMMA分子链的速度自相关系数在保压模拟的初期以指数的形式迅速衰减,当运行到大约4.1 ps后衰减速度逐渐变缓,到8.3 ps时其速度自相关系数逐渐趋近于0,之后在0值附近存在微弱的波动,说明在8.3 ps后纳米型腔内PMMA分子链的平动速度已经同模拟初期不再相关。聚合物的内应力逐渐衰减并最终趋近于稳定,即是宏观上PMMA片材在保压阶段所发生应力松弛现象的微观反映。将均方回转半径和速度相关系数的变化趋势与实际PMMA在类固态等温热压印应力松弛实验中松弛模量随时间的变化趋势作对比,也有很好的一致性[20]。
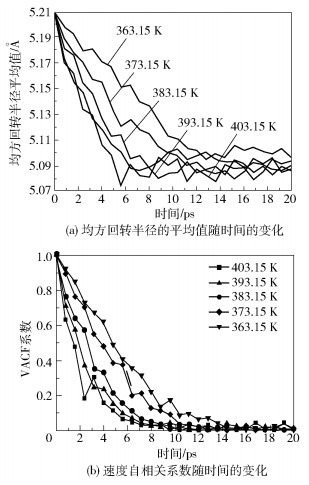
2.2.4 温度对聚合物高分子链均方回转半径以及平动速度自相关系数的影响均方回转半径的平均值在不同温度下随时间的变化情况以及平动速度自相关系数在不同温度下随时间的变化情况如图 11所示。
|
图 11 不同温度下模具镍层型腔内PMMA分子链均方回转半径的平均值与速度自相关系数随时间的变化 Fig.11 Variation of the average mean square radius of gyration and velocity autocorrelation coefficient of PMMA molecular chains in the cavity of the mold nickel layer with time at different temperatures |
从图 11可以得知,处于不同温度下PMMA分子链均方回转半径的平均值均随着模拟时间的增加而逐渐减小,并且减小的速度逐渐变缓。随着温度的降低,其回转半径平均值减小的幅度变得更小,并且减小的速率相比于较高温度也变得更低。不同温度下PMMA分子链的平动速度自相关系数同样随着模拟时间的增加而逐渐衰减。当温度较高时其速度自相关系数衰减的速度较快,之后逐渐趋近于0并且存在着微弱波动;随着温度的降低,PMMA分子链的自相关系数衰减的速度逐渐变缓,需要更长的时间接近0值并且波动幅度更小。说明当温度较低时纳米型腔内的PMMA分子链的平动速度在更长的时间内都具有一定的相关性。
在不同的温度下模具镍层型腔内的PMMA分子链均方回转半径的平均值以及平动速度自相关系数随时间的变化趋势,正是宏观上聚合物时温等效原理的微观体现,即增加反应时间以及提高反应温度对于分子的运动过程而言是等效的。在实际的热压成形过程中,为了得到具有高复制率、完整微纳米结构的聚合物材料,既要考虑不同温度对于不同种类的聚合物和模具之间相互作用能的影响,又要考虑保压阶段聚合物松弛过程的快慢。
3 结论(1) 在热压过程的填充阶段,对体系能量和分子的平均密度计算和分析结果表明,总能量、势能、非键能和动能随时间的变化逐步趋于稳定,分子平均密度随时间变化逐渐增大,并趋于稳定,说明PMMA分子链段的运动由活跃趋向于平稳,整个体系进入稳定状态。
(2) 在保压松弛阶段,PMMA分子链的均方回转半径平均值、速度分布函数以及速度自相关函数系数均呈现随时间迅速衰减至稳定的变化规律,即从分子链尺寸变化与分子链段运动速度的角度对聚合物的应力松弛现象进行了微观解释。
(3) 在不同的温度条件下,PMMA分子链均方回转半径的平均值以及平动速度自相关系数随时间的变化逐步趋于稳定,并且温度越高,衰减越快,从分子运动的角度验证了时温等效原理。
| [1] |
Gad-el-Hak M. Flow physics in MEMS[J]. Mécanique & Industries, 2001, 2(4): 313-341. |
| [2] |
Hossain D, Tschopp M A, Ward D K, et al. Molecular dynamics simulations of deformation mechanisms of amorphous polyethylene[J]. Polymer, 2010, 51(25): 6071-6083. DOI:10.1016/j.polymer.2010.10.009 |
| [3] |
Araki K, Yasuda M, Horiba A, et al. Computational study on polymer filling process in nanoimprint lithography for bi-layered resist[J]. Mrs Proceedings, 2013, 1499(8): 2188-2191. |
| [4] |
Yang S, Yu S, Cho M. Influence of mold and substrate material combinations on nanoimprint lithography process:MD simulation approach[J]. Applied Surface Science, 2014, 301(19): 189-198. |
| [5] |
Cheng M C, Sung C K, Wang W H. The effects of thin-film thickness on the formation of metallic patterns by direct nanoimprint[J]. Journal of Materials Processing Technology, 2007, 191(1): 326-330. |
| [6] |
Pei Q X, Lu C, Liu Z S, et al. Molecular dynamics study on the nanoimprint of copper[J]. Journal of Physics D:Applied Physics, 2007, 40(16): 4928-4935. DOI:10.1088/0022-3727/40/16/026 |
| [7] |
Woo Y S, Lee D E, Lee W I. Molecular dynamic studies on deformation of polymer resist during thermal nano imprint lithographic process[J]. Tribology Letters, 2009, 36(3): 209-222. DOI:10.1007/s11249-009-9474-y |
| [8] |
熊孝东, 魏正英, 杜军, 等. 纳米压印中聚合物界面行为的分子动力学[J]. 高分子材料科学与工程, 2011, 27(6): 186-190. Xiong X D, Wei Z Y, Du J, et al. Molecular dynamics of polymer's interface behavoious in the nanoimprint lithography[J]. Polymer Materials Science & Engineering, 2011, 27(6): 186-190. (in Chinese) |
| [9] |
杨振洲. 聚合物微结构平板热压印成型工艺的研究[D]. 北京: 北京化工大学, 2015. Yang Z Z. The study of polymer micro-structure plate to plate hot embossing process[D]. Beijing: Beijing University of Chemical Technology, 2015. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10010-1015725342.htm |
| [10] |
Wu D M, Sun J Y, Liu Y, et al. Rapid fabrication of microstructure on PMMA substrate by the plate to plate transition-spanning isothermal hot embossing method nearby glass transition temperature[J]. Polymer Engineering and Science, 2017, 57(3): 268-274. DOI:10.1002/pen.v57.3 |
| [11] |
孙靖尧, 吴大鸣, 刘颖, 等. 聚合物微纳制造技术[J]. 橡塑技术与装备, 2016, 42(10): 1-9. Sun J Y, Wu D M, Liu Y, et al. Polymer micro-nano manufacturing technology[J]. China Rubber/Plastics Technology and Equipment, 2016, 42(10): 1-9. (in Chinese) |
| [12] |
Yang S, Yu S, Cho M. Influence of mold and substrate material combinations on nanoimprint lithography process:MD simulation approach[J]. Applied Surface Science, 2014, 301(19): 189-198. |
| [13] |
Sun H. COMPASS:An ab initio force-field optimized for condensed-phase applications-overview with details on alkane and benzene compounds[J]. Journal of Physical Chemistry B, 1998, 102(38): 7338-7364. DOI:10.1021/jp980939v |
| [14] |
Sun H. Ab initio calculations and force field development for computer simulation of polysilanes[J]. Macromolecules, 1995, 28(3): 701-712. DOI:10.1021/ma00107a006 |
| [15] |
Kittel C. Introduction to solid state physics. 2nd ed[M]. New York: John Wiley & Sons, Inc., 1956: 547-548.
|
| [16] |
Yamamoto T. Molecular dynamics modeling of polymer crystallization from the melt[J]. Polymer, 2004, 45(4): 1357-1364. DOI:10.1016/j.polymer.2003.04.006 |
| [17] |
Koyama A, Yamamoto T, Fukao K, et al. Molecular dynamics studies on local ordering in amorphous polyethylene[J]. Journal of Chemical Physics, 2001, 115(1): 560-566. DOI:10.1063/1.1378068 |
| [18] |
Yashiro K, Ito T, Tomita Y. Molecular dynamics simulation of deformation behavior in amorphous polymer:nucleation of chain entanglements and network structure under uniaxial tension[J]. International Journal of Mechanical Sciences, 2003, 45(11): 1863-1876. DOI:10.1016/j.ijmecsci.2003.11.001 |
| [19] |
Mondello M, Grest G S. Molecular dynamics of linear and branched alkanes[J]. Journal of Chemical Physics, 1995, 103(16): 7156-7165. DOI:10.1063/1.470344 |
| [20] |
王琦, 吴大鸣, 刘颖, 等. PMMA近玻璃化转变温度下应力松弛特性分析[J]. 塑料, 2017(2): 5-8. Wang Q, Wu D M, Liu Y, et al. The analysis of stress-strain behavior of PMMA near glass transition temperature[J]. Plastic, 2017(2): 5-8. (in Chinese) |








