在过去的几十年中,单螺杆挤出机一直是聚合物加工最重要的设备之一,由于设计和操作的需要,对其流体流动的数值模拟研究一直是热点问题[1]。
单螺杆挤出机内的熔体流动的数学模型一般为非牛顿流体的流动与热传导的耦合的非线性偏微分方程组定解问题[2],而且求解区域随时间变化,结构复杂。对此模型的数值求解通常用有限元[3]等方法或简化为更低维模型求解,但要较精确高效地求解非常困难,主要困难来源于求解区域的复杂性。
单螺杆挤出机流体流动区域一般由机筒及螺杆组成,其中机筒内的螺杆还按一定的角速度旋转。为了克服求解区域的复杂带来的困难,文献[4]和[5]利用不同的变换(类似于拉直)将螺槽区域变换为柱体区域,从而简化了问题的计算,但难以应用于包含漏流层情形。
一般单螺杆挤出机都有漏流层,其流体流动区域的截面是一个二维双连通区域,通常其外边界曲线为圆周,内边界曲线(也称为螺杆的端面曲线)依螺槽的形状而不同,可以是比较复杂的曲线。对于均匀变化的螺杆或螺杆中均匀变化的一段,其不同截面可看成是由一个截面沿同一轴心旋转不同角度所形成。因此,若将每一横截面通过适当的变换变为相同的圆环形区域,则单螺杆挤出机流体流动区域就变为圆环柱形区域,从而使得求解区域不仅与时间无关,而且成为较规则的三维区域,非常便于计算包含漏流层的单螺杆挤出机流体流动问题。为了使得变换光滑,且变换后的方程尽可能简洁,共形变换[6-8]是一种较好的变换方法。
对于不可压缩流体流动问题,近年来兴起的投影算法[9]是一个相对高效的算法,其核心步骤是求解流动区域上的泊松方程。为了说明将共形变换应用于投影算法计算单螺杆挤出机流体流动问题时可较大简化问题的计算,本文以端面曲线为椭圆的单螺杆挤出机为例,计算了其流动区域上的三维泊松方程定解问题[4],并与精确解作了比较。计算结果表明,此方法简单有效。
1 共形映射的计算通过共形映射[8]使得区域规则化的方法有很多种,本文借鉴文献[6]的方法计算单螺杆挤出机流体流动区域截面到圆环区域的共形映射。
1.1 理论公式在复变函数理论中,有以下熟知的结论[6]。
定理1 如果h在复平面区域Ω上是单值解析函数,且在Ω∪Γ连续,Γ为Ω的边界且Γ是光滑的,则有
| $ \frac{1}{{2{\rm{\pi i}}}}\int_\mathit{\Gamma } {\frac{{h\left( w \right)}}{{w - z}}{\rm{d}}w = \frac{1}{2}h\left( z \right),z \in \mathit{\Gamma }} $ | (1) |
设Ω为双连通区域,Ω的边界为Γ,方程为z=z(t)。其中外边界为Γ0,方程为z=z0(t);内边界为Γ1,方程为z=z1(t)。理论上,对任一双连通区域,存在单值解析函数将其映射为同心圆环区域。设映射函数为f(z),且f(z0(t))=eiθ0(t), f(z1(t))=μ1eiθ1(t),即f将Γ0映为单位圆周,将Γ1映为半径μ1的圆周(1/μ1为Ω的模,是个待定的参数),从而f将Ω映射为同心圆环。若能解出θ0(t), θ1(t)和μ1,则利用Cauchy积分公式即可得到f(z)。
利用定理1, 加上适当的推导,对于双连通区域,可得到
| $ \begin{array}{l} \;\;\;\;\;\;\;g\left( {{z_0}} \right) + \int_{{\mathit{\Gamma }_0}} {N\left( {{z_0},w} \right)g\left( w \right)\left| {{\rm{d}}w} \right|} - \int_{ - {\mathit{\Gamma }_1}} {{P_0}\left( {{z_0},} \right.} \\ \left. w \right)g\left( w \right)\left| {{\rm{d}}w} \right| = 0,{z_0} \in {\mathit{\Gamma }_0} \end{array} $ | (2) |
| $ \begin{array}{l} \;\;\;\;\;\;\;g\left( {{z_1}} \right) + \int_{{\mathit{\Gamma }_0}} {{P_1}\left( {{z_1},w} \right)g\left( w \right)\left| {{\rm{d}}w} \right|} - \int_{ - {\mathit{\Gamma }_1}} {N\left( {{z_1},} \right.} \\ \left. w \right)g\left( w \right)\left| {{\rm{d}}w} \right| = 0,{z_1} \in {\mathit{\Gamma }_1} \end{array} $ | (3) |
其中T(z)=z(t)/|z′(t)|, g(z)=T(z)f′(z),P0(z, w)、P1(z, w)、N(z, w)是与z、w、T(z)、μ1相关的函数。
为了保证唯一性,可设f(z0(0))=1, 即
| $ \left\{ \begin{array}{l} {\mathop{\rm Re}\nolimits} \left[ {g\left( {{z_0}\left( 0 \right)} \right)} \right] = 0\\ {\mathop{\rm Im}\nolimits} \left[ {g\left( {{z_0}\left( 0 \right)} \right)/\left| {g\left( {{z_0}\left( 0 \right)} \right)} \right|} \right] = 1 \end{array} \right. $ | (4) |
最后基于边界对应函数的单调递增性,有
| $ \left\{ \begin{array}{l} \int_0^{2{\rm{\pi }}} {\left| {g\left( {{z_0}\left( 0 \right)} \right){{z'}_0}\left( t \right)} \right|{\rm{d}}t} = \int_0^{2{\rm{\pi }}} {{{\theta '}_0}\left( t \right){\rm{d}}t} = 2{\rm{\pi }}\\ \int_0^{2{\rm{\pi }}} {\left| {g\left( {{z_1}\left( t \right)} \right){{z'}_1}\left( t \right)} \right|{\rm{d}}t} = 2{\rm{\pi }}{\mu _1} \end{array} \right. $ | (5) |
设参数t的变化范围为[0, 2π]。在Γ0上对t等距离散n个点,在Γ1上对t等距离散m个点,用梯形法则的Nystrom方法将式(2)~(5) 离散化,得到
| $ \left( {\begin{array}{*{20}{c}} {{\mathop{\rm Re}\nolimits} A}&{ - {\mathop{\rm Im}\nolimits} A}\\ {{\mathop{\rm Im}\nolimits} A}&{{\mathop{\rm Re}\nolimits} A} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\mathop{\rm Re}\nolimits} x}\\ {{\mathop{\rm Im}\nolimits} x} \end{array}} \right) = \left( \begin{array}{l} 0\\ 0 \end{array} \right) $ | (6) |
| $ \sum\limits_{j = 1}^m {\left( {{\mathop{\rm Re}\nolimits} {x_{1\tilde j}} + {\rm{i}}{\mathop{\rm Im}\nolimits} {x_{1\tilde j}}} \right)} = 0 $ | (7) |
| $ \sum\limits_{j = 1}^n {\sqrt {{{\left( {{\mathop{\rm Re}\nolimits} {x_{0j}}} \right)}^2} + {{\left( {{\mathop{\rm Im}\nolimits} {x_{0j}}} \right)}^2}} } = n $ | (8) |
| $ \sum\limits_{\tilde j = 1}^m {\sqrt {{{\left( {{\mathop{\rm Re}\nolimits} {x_{1\tilde j}}} \right)}^2} + {{\left( {{\mathop{\rm Im}\nolimits} {x_{1\tilde j}}} \right)}^2}} } = m{\mu _1} $ | (9) |
| $ {\mathop{\rm Re}\nolimits} {x_{01}} = 0 $ | (10) |
| $ {\mathop{\rm Im}\nolimits} \left[ {{x_{01}}/\sqrt {{{\left( {{\mathop{\rm Re}\nolimits} {x_{01}}} \right)}^2} + {{\left( {{\mathop{\rm Im}\nolimits} {x_{01}}} \right)}^2}} } \right] = 1 $ | (11) |
其中x0j=|z′0(tj)|g(z0(tj))(j=1, 2, …, n),
x分量的实部和虚部加上参数μ1,共有2(m+n)+1个未知量,式(6)~(11) 共有2(m+n)+5个方程,所以此方程组为超定方程组,可采用最小二乘法求解。
解出x后,即可求得θ0(t)、θ1(t),从而得到边界上的点在映射f下的值。对于内部的点,利用柯西积分可计算出f的值,即
| $ \begin{array}{l} \;\;\;\;\;\;\;f\left( {zz} \right) = \frac{1}{{2{\rm{\pi i}}}}\int_0^{2{\rm{\pi }}} {\frac{{f\left( {{z_0}\left( t \right)} \right)}}{{{z_0}\left( t \right) - zz}}{{z'}_0}\left( t \right){\rm{d}}t} - \frac{1}{{2{\rm{\pi i}}}}\int_0^{2{\rm{\pi }}} {} \\ \frac{{f\left( {{z_1}\left( t \right)} \right)}}{{{z_1}\left( t \right) - zz}}{{z'}_1}\left( t \right){\rm{d}}t,zz \in \mathit{\Omega } \end{array} $ |
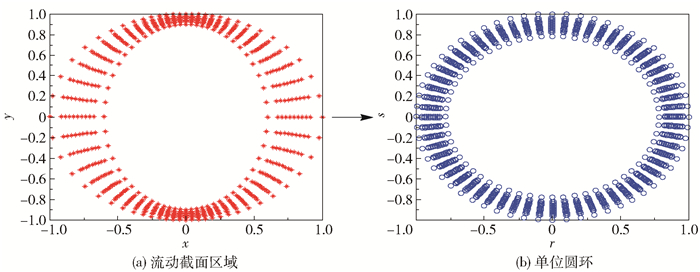
以Ω的外边界为单位圆周,内边界为椭圆周为例进行了计算,用大范围信赖域方法求解式(6)~(11) 构成的超定方程组的非线性最小二乘问题。当内边界椭圆长半轴为0.9、短半轴为0.6时,取m=n=48,计算得到μ1=0.783176;计算的最优结果下,最小二乘的残差平方和为4.136×10-9。图 1为计算结果图形。可以看出,此方法能得到较高精度的共形映射。
|
图 1 流动截面区域到圆环的共形变换 Fig.1 Contrast map before and after conformal mapping |
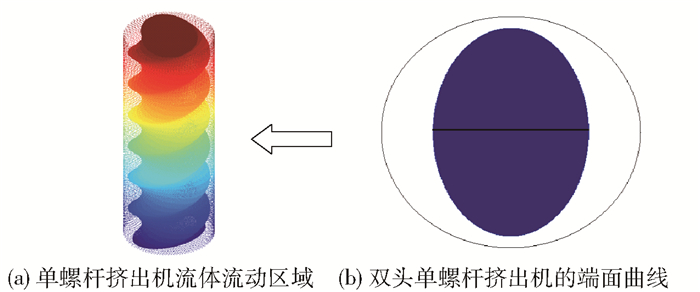
对于均匀变化的螺杆或螺杆中均匀变化的一段,其不同截面可看成是由一个截面沿同一轴心旋转不同角度形成,如图 2所示。将每个截面通过第1章的共形变换变为相同的圆环形区域,则单螺杆挤出机流体流动区域就变为圆环柱形区域。
|
图 2 旋转变换示意图 Fig.2 Rotation transformation diagram |
设机筒为圆柱面,螺杆的轴心与机筒的轴心一致,以此轴心为z轴,z=0为流体进口的横截面,并取其为xOy坐标面,建立直角坐标系{O, x, y, z}。以挤出机的螺槽是单线螺槽的情况为例,螺距为H0。当z=0时,共形映射f将流体流动截面区域Ω0映射为圆环形区域D。取b=H0/(2π), 则螺杆表面可看成是Ω0的内边界Γ1随z的增大而绕z轴沿逆时针方向旋转角度z/b得到的,且当z=H0时恰好转过2π弧度角;当z=h时, 流体流动截面区域Ωh也可看成是Ω0绕z轴旋转角度h/b得到。这样,流体流动区域G上的变换可以取为
| $ \left\{ \begin{array}{l} \xi = {\mathop{\rm Re}\nolimits} \left( {{{\rm{e}}^{{\rm{i}}g\left( {x,y,z} \right)}}f\left( {\left( {x + {\rm{i}}y} \right){{\rm{e}}^{ - {\rm{i}}z/b}}} \right)} \right)\\ \eta = {\mathop{\rm Im}\nolimits} \left( {{{\rm{e}}^{{\rm{i}}g\left( {x,y,z} \right)}}f\left( {\left( {x + {\rm{i}}y} \right){{\rm{e}}^{ - {\rm{i}}z/b}}} \right)} \right)\\ h = z \end{array} \right. $ | (12) |
其中g(x, y, z)可取为任意的实值光滑函数。这时,区域G就变为{ξ, η, h}下的圆环柱体区域。若G={(x, y, z)|(x, y)∈Ωz, 0≤z≤H},对{ξ, η, h}再作柱坐标变换
| $ \xi = r\cos s,\eta = r\sin s,h = h $ | (13) |
则G变为{r, s, h}坐标下的长方体区域。
3 求解泊松方程为了说明第二章的三维变换对求解复杂的单螺杆挤出机三维流体流动区域G上的偏微分方程有效和简便[10],以端面曲线为椭圆的单螺杆挤出机为例,应用该变换求解G上的Dirichlet问题,并与精确解作比较。
3.1 问题变换与计算方法设G={(x, y, z)|(x, y)∈Ωz, 0≤z≤H},在G区域上所求解的问题为:
| $ \left\{ \begin{array}{l} {U_{xx}} + {U_{yy}} + {U_{zz}} = p\left( {x,y,z} \right)\\ U\left| {_{\partial G} = q\left( {x,y,z} \right)} \right. \end{array} \right. $ | (14) |
设H0为螺距,b=H0/2π为参数,Ω0为进口(z=0) 处的流体流动截面区域,则Ωz为Ω0绕z轴逆时针旋转角度z/b得到的流体流动截面区域。设Ω0的外边界为单位圆周,参数方程为x=cos t和y=sin t(t∈[0, 2π]); 内边界为椭圆周,其方程为x=ccos t和y=dsin t(t∈[0, 2π]),其中c, d > 0为椭圆的两个半轴长。
设共形映射f将Ω0映成内半径为μ1、外半径为1的圆环区域,且取
| $ \left\{ \begin{array}{l} \xi = {\mathop{\rm Re}\nolimits} \left( {{{\rm{e}}^{{\rm{i}}z/b}}f\left( {\left( {x + {\rm{i}}y} \right){{\rm{e}}^{ - {\rm{i}}z/b}}} \right)} \right)\\ \eta = {\mathop{\rm Im}\nolimits} \left( {{{\rm{e}}^{{\rm{i}}z/b}}f\left( {\left( {x + {\rm{i}}y} \right){{\rm{e}}^{ - {\rm{i}}z/b}}} \right)} \right)\\ h = z \end{array} \right. $ | (15) |
则此变换将G映射成内半径为μ1、外半径为1、高为H的圆环柱V。进一步作式(13) 所示的柱坐标变换,设变量复合后变换为
| $ \left\{ \begin{array}{l} r = r\left( {x,y,z} \right)\\ s = s\left( {x,y,z} \right)\\ h = z \end{array} \right. $ | (16) |
则G变换为{r, s, h}坐标下的长方体区域B=[μ1, 1]×[0, 2π]×[0, H], 问题(14) 变成
| $ \left\{ \begin{array}{l} {a_{11}}{U_{rr}} + {a_{21}}{U_{ss}} + {a_{33}}{U_{hh}} + 2{a_{12}}{U_{rs}} + 2{a_{13}}{U_{rh}} + \\ \;\;\;\;\;\;\;2{a_{23}}{U_{sh}} + {b_1}{U_r} + {b_2}{U_s} + {b_3}{U_h} + cU = \\ \;\;\;\;\;\;\;\tilde p\left( {r,s,h} \right)\left( {\left( {r,s,h} \right) \in B} \right)\\ U\left| {_{r = {\mu _1}} = {g_{1a}}\left( {s,h} \right)} \right.,U\left| {_{r = 1} = {g_{1b}}\left( {s,h} \right)} \right.\\ U\left| {_{s = 0}} \right. = U\left| {_{s = 2{\rm{\pi }}}} \right.,{U_s}\left| {_{s = 0}} \right. = {U_s}\left| {_{s = 2{\rm{\pi }}}} \right.\\ U\left| {_{h = 0} = {g_{3a}}\left( {r,s} \right)} \right.,U\left| {_{h = H} = {g_{3b}}\left( {r,s} \right)} \right. \end{array} \right. $ | (17) |
其中a11=rx2+ry2+rz2, a22=sx2+sy2+sz2, a33=hx2+hy2+hz2=1, a12=rxsx+rysy+rzsz, a13=rxhx+ryhy+rzhz=rz, a23=sxhx+syhy+szhz=sz, b1=rxx+ryy+rzz, b2=sxx+syy+szz, b3=hxx+hyy+hzz=0, c=0
式(17) 的方程形式虽然比式(14) 复杂,但不会产生实质性困难,反而因为复杂的求解区域变成了简单的长方体区域,可方便地用差分方法求解,极大地简化了问题的计算。
计算步骤如下:
1) 计算共形映射f 得到θ0(t), θ1(t)和μ1后,以样条函数形式给出w0(t)=f(z0(t))=eiθ0(t)和w1(t)=f(z1(t))=μ1eiθ1(t);
2) 计算x=x(r, s, h)和y=y(r, s, h) 因为f的逆映射f-1也是解析函数,可利用Cauchy公式给出f-1,进一步,由
| $ x + {\rm{i}}y = {{\rm{e}}^{{\rm{i}}h/b}}{f^{ - 1}}\left( {\left( {r\cos s + {\rm{i}}r\sin s} \right){{\rm{e}}^{ - {\rm{i}}h/b}}} \right) $ |
计算出x=x(r, s, h)和y=y(r, s, h),并以三元样条函数形式给出;
3) 对式(17) 离散计算 采用等步长中心差分格式,得到的线性方程组用块追赶法求解。
3.2 数值计算结果设精确解为Ue=1+x2y+sin z,先计算出相应的p(x, y, z)=2y-sinz和q(x, y, z),然后分别就c=0.5, d=0.8和c=0.6, d=0.9对式(17) 进行计算。令Uij=maxk{|Uijk-Ueijk|},其中Uijk为U(ri, sj, hk)的计算值,Ueijk为Ue(ri, sj, hk)的值。
计算误差的情况如下。
1) c=0.5, d=0.8
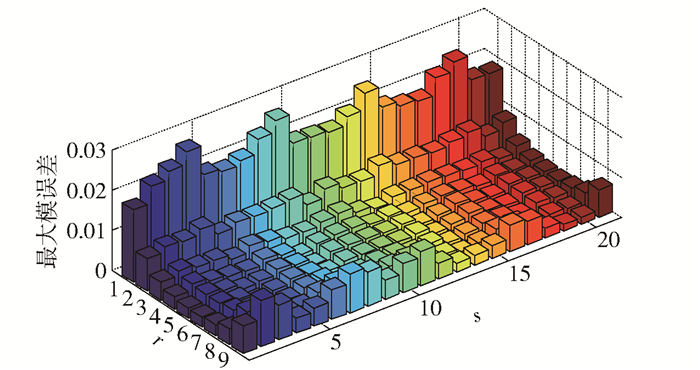
当(r, s, h)网格数取为5×10×100时,最大模误差为0.02793,均方根误差为0.00534;网格数取为10×20×200时,最大模误差为0.02748,均方根误差为0.00145。h方向的最大模误差分布如图 3所示。
|
图 3 c=0.5, d=0.8时最大模误差分布图 Fig.3 Maximum modulus error distribution when c=0.5, and d=0.8 |
2) c=0.6, d=0.9
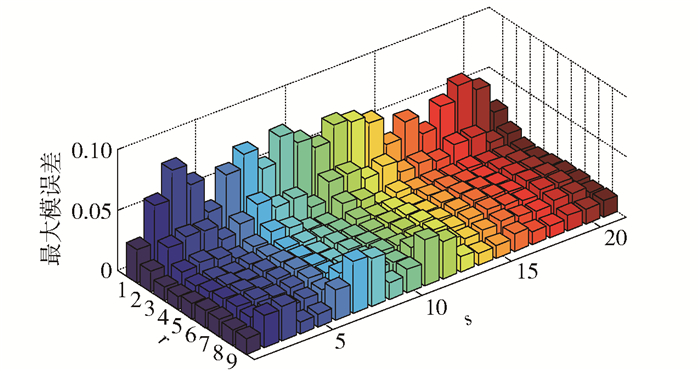
当(r, s, h)网格数取为5×10×200时,最大模误差为0.10456,均方根误差为0.00862;网格数取为10×20×400时,最大模误差为0.08182,均方根误差为0.00497。h方向的最大模误差分布如图 4所示。
|
图 4 c=0.6, d=0.9时最大模误差分布图 Fig.4 Maximum modulus error distribution when c=0.6, and d=0.9 |
通过本文所述的共形变换将流动区域的截面变为圆环形区域,再构造三维区域变换,可以将单螺杆挤出机流体流动区域变为圆环柱形区域,从而使得求解区域不仅与时间无关,而且变成了较规则的三维区域,大大便于问题的计算;对此这类区域上的三维泊松方程进行数值实验的结果表明,此方法简单有效。当使用投影算法求解不可压缩流体流动问题时,利用本文方法求解核心步骤中的泊松方程,可以使投影算法更为简便高效。
| [1] |
Li Y, Heish F. Modeling of flow in a single screw extruder[J]. Journal of Food Engineering, 1996, 27(4): 353-375. DOI:10.1016/0260-8774(95)00016-X |
| [2] |
石宗宝. 非线性偏微分方程组的定解问题[J]. 湖南师范大学自然科学学报, 1980(2): 7-14. Shi Z B. The solution of nonlinear partial differential equations[J]. Journal of Natural Science of Hunan Normal University, 1980(2): 7-14. (in Chinese) |
| [3] |
Chiruvella R V, Jaluria Y, Karwe M V. Numerical simulation of the extrusion process for food materials in a single-screw extruder[J]. Journal of Food Engineering, 1996, 30(3/4): 449-467. |
| [4] |
王国娟, 黄晋阳. 螺槽区域上偏微分方程模型的几何变换算法[J]. 北京化工大学学报:自然科学版, 2016, 43(5): 118-122. Wang G J, Huang J Y. A geometric transformation algorithm for PDE models on a screw channel domain[J]. Journal of Beijing University of Chemical Technology:Natural Science, 2016, 43(5): 118-122. (in Chinese) |
| [5] |
伍继梅. 单螺杆挤出机三维数值模拟的研究[D]. 北京: 北京化工大学, 2014. Wu J M. The study on the 3-dimensional numerical simulation of single screw extuder[D]. Beijing:Beijing University of Chemical Technology, 2014.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10010-1015581194.htm |
| [6] |
Murid A H M, Hu L N. Numerical conformal mapping of bounded multiply connected regions by an integral equation method[J]. Int J Contemp Math Sciences, 2009, 4(23): 1121-1147. |
| [7] |
Deglaire P, Agren O, Bernhoff H, et al. Conformal mapping and efficient boundary element method without boundary elements for fast vortex particle simulations[J]. European Journal of Mechanics-B/Fluids, 2008, 27(2): 150-176. DOI:10.1016/j.euromechflu.2007.03.005 |
| [8] |
Turner M R, Bridges T J, Ardakani H A. The pendulum-slosh problem:simulation using a time-dependent conformal mapping[J]. Journal of Fluids & Structures, 2015, 59: 202-223. |
| [9] |
倪诗浩, 田振夫. 求解非定常不可压Navier-Stokes方程的一种高精度并行算法[J]. 复旦学报:自然科学版, 2016, 55(3): 315-320. Ni S H, Tian Z F. To solve the unsteady incompressible Navier-Stokes equations in a kind of high precision parallel algorithm[J]. Journal of Fudan University:Natural Science, 2016, 55(3): 315-320. (in Chinese) |
| [10] |
徐百平, 瞿金平, 刘跃军, 等. 单螺杆挤出机中三维流动有限体积数值模拟[J]. 化工学报, 2008, 59(12): 3055-3060. Xu B P, Qu J P, Liu Y J, et al. Numerical simulation of three-dimensional flow in single screw extruder by finite volume method[J]. Journal of Chemical Industry and Engineering, 2008, 59(12): 3055-3060. (in Chinese) DOI:10.3321/j.issn:0438-1157.2008.12.014 |








