引言

通常情况下，随机噪音对系统的稳定性有一定影响，有些不稳定的常微分系统在加入随机噪音后会变得稳定，因此许多学者开始研究随机噪音稳定化理论。Khasminskii^[1]在随机噪音稳定化方面的研究结果具有开创性意义，他通过增加两个随机噪音项使得二维线性的不稳定系统达到稳定。此后，与其相关的部分问题也陆续地得到了解决。Mao^[2-3]选用布朗运动作为随机因素，对随机微分方程的稳定性进行了详细的介绍，并建立了随机稳定化的一般理论；Caraballo等^[4]研究了随机微分方程一般衰减速度的几乎处处稳定性以及确定的偏微分系统的稳定化问题；Wu等^[5-6]分别研究带有两个随机项的非线性系统和非线性时滞系统的正则化(suppression)和稳定化问题，加入的两个独立的随机项中，一项保证整体解的存在性，另一项保证系统的稳定性。

上述研究都对漂移项系数有着严格的增长性限制。针对这一问题，Li等^[7]研究了在更为一般的增长条件下非线性系统的超指数以及一般衰减速度的几乎处处稳定问题，却没有考虑相应的时滞系统的稳定性。基于此，本文考虑非线性时滞系统的稳定化问题，并建立随机时滞系统以一般衰减速度几乎处处稳定的判定定理，来解决时滞系统的稳定化问题。

1 基本假设与定义

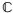
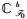
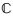
设(Ω, $\mathscr{F}$ , P)为完备的概率空间，且带有满足通常条件的子流{ $\mathscr{F}_t$ }_t≥0，即{ $\mathscr{F}_t$ }_t≥0是右连续的且 $\mathscr{F}_0$ 包含所有的零测集。令n, m∈ $\mathbb{N}$ , 对任意给定的τ>0, ([－τ, 0]; $\mathbb{R}$ ⁿ)表示从[-τ，0]到 $\mathbb{R}$ ⁿ的连续函数的集合，且范数为|·|表示 $\mathbb{R}$ ⁿ中的欧氏范数；([－τ, 0]; $\mathbb{R}$ ⁿ)表示几乎所有有界的 $\mathscr{F}_0$ 可测的函数族。若x(t)表示在t≥0上连续的 $\mathbb{R}$ ⁿ值的随机过程，则X_t={x(t+s):－τ≤s≤0}(t≥0) 是属于([－τ, 0]; $\mathbb{R}$ ⁿ)的随机过程。

考虑以下随机时滞微分系统

$ {\rm{d}}\mathit{\boldsymbol{x}}\left( t \right) = f\left( {\mathit{\boldsymbol{x}}\left( t \right),\mathit{\boldsymbol{x}}\left( {t - \tau } \right),t} \right){\rm{d}}t + g\left( {\mathit{\boldsymbol{x}}\left( t \right),\mathit{\boldsymbol{x}}\left( {t - \tau } \right),t} \right){\rm{d}}B\left( t \right) $

(1)

其中x(t)=[x₁(t), …, x_n(t)]^T∈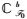 $\mathbb{R}$ ⁿ，且定义初值为x₀=ξ∈([－τ, 0]; $\mathbb{R}$ ⁿ)；B(t)是定义在空间(Ω, $\mathscr{F}$ , P)上的m维的布朗运动；漂移项系数f: $\mathbb{R}$ ⁿ× $\mathbb{R}$ ⁿ× $\mathbb{R}$ ₊→ $\mathbb{R}$ ⁿ和扩散项系数g: $\mathbb{R}$ ⁿ× $\mathbb{R}$ ⁿ× $\mathbb{R}$ ₊→ $\mathbb{R}$ ^n×m均为连续函数，且满足f(0, 0, t)≡0, g(0, 0, t)≡0。显然，式(1) 有平凡解x(t)≡0。

为保证式(1) 解的存在唯一性，给定如下的局部Lipschitz条件：

假设1 对任意T≥0和任意k∈ $\mathbb{Z}$ ₊，存在正常量C_{k, T}>0，使得

$ \begin{array}{l} \;\;\;\;\;\;\;\left| {f\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}},t} \right) - f\left( {\mathit{\boldsymbol{x'}},\mathit{\boldsymbol{y'}},t} \right)} \right| \vee \left| {g\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}},t} \right) - g\left( {\mathit{\boldsymbol{x'}},} \right.} \right.\\ \left. {\left. {\mathit{\boldsymbol{y'}},t} \right)} \right| \le {C_{k,T}}\left( {\left| {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{x'}}} \right| + \left| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{y'}}} \right|} \right) \end{array} $

(2)

对任意0≤t≤T和|x|∨|x′|∨|y|∨|y′|≤k成立，其中a∨b表示max {a, b}。

引理1 ^[8]若假设1成立，则对任意初值x₀=ξ(∈ $C_{\mathscr{F}_0}^b$ ([－τ, 0]; $\mathbb{R}$ ⁿ))，式(1) 在t∈[0, τ_e)上有唯一的最大局部强解。其中τ_e是解的爆炸时间，即τ_e=inf {t≥0, |x(t)|=∞}。

下面给出几乎处处稳定性的定义。

定义1 设函数λ(t)∈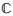( $\mathbb{R}$ ₊; $\mathbb{R}$ ₊)单调递增，且满足t→∞时，λ(t)→∞，若式(3)

$ \mathop {\lim }\limits_{t \to + \infty } \sup \frac{{\ln \left| {\mathit{\boldsymbol{x}}\left( t \right)} \right|}}{{\ln \lambda \left( t \right)}} \le - \gamma \;{\rm{a}}{\rm{.}}\;{\rm{s}}. $

(3)

对任意初值ξ∈ $C_{\mathscr{F}_0}^b$ ([－τ, 0]; $\mathbb{R}$ ⁿ)均成立，则称式(1)(或式(1) 的平凡解)以一般衰减速度λ(t)几乎处处稳定，阶为γ。

2 主要结果及证明

考虑非线性系统：

$ {\rm{d}}\mathit{\boldsymbol{x}}\left( t \right) = f\left( {\mathit{\boldsymbol{x}}\left( t \right),\mathit{\boldsymbol{x}}\left( {t - \tau } \right),t} \right){\rm{d}}t $

(4)

其中x∈ $\mathbb{R}$ ⁿ且初值x₀=ξ∈C([－τ, 0]; $\mathbb{R}$ ⁿ)，f: $\mathbb{R}$ ⁿ× $\mathbb{R}$ ⁿ× $\mathbb{R}$ ₊→ $\mathbb{R}$ ⁿ是连续函数，满足条件f(0, 0, t)≡0。

假设时滞微分系统式(4) 是不稳定的，则需要引入合适的随机噪音使其稳定。

2.1 非线性随机时滞系统的构造

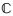
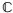
首先，给定一元函数h∈( $\mathbb{R}$ ₊; $\mathbb{R}$ ₊)和n元函数γ, δ∈( $\mathbb{R}$ ⁿ; $\mathbb{R}$ ₊)。为研究式(4) 的稳定化问题，对f施加以下假设条件：

假设2 存在未知常数θ>0，使得式(5)

$ {\mathit{\boldsymbol{x}}^{\rm{T}}}f\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}},t} \right) \le \theta h\left( t \right)\left( {\gamma \left( \mathit{\boldsymbol{x}} \right) + \delta \left( \mathit{\boldsymbol{y}} \right)} \right){\left| \mathit{\boldsymbol{x}} \right|^2} $

(5)

对于任意的t>0和x, y∈ $\mathbb{R}$ ⁿ成立。

当式(5) 成立时，式(4) 包含文献[7]中定义的“serious parameter unknowns”(重要参量未知)和“serious time-variations”(重要时间变量)。值得注意的是，同样研究时滞系统稳定性的文献[6]中，对系统的漂移项施加了单边多项式增长的条件

$ {\mathit{\boldsymbol{x}}^{\rm{T}}}f\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}},t} \right) \le \left( {\gamma + \kappa {{\left| \mathit{\boldsymbol{x}} \right|}^\alpha } + \kappa '{{\left| \mathit{\boldsymbol{y}} \right|}^\alpha }} \right){\left| \mathit{\boldsymbol{x}} \right|^2} $

(6)

其中κ, κ′, α和γ为非负常数。

显然式(6) 是式(5) 的特殊情况。当函数f(x, y, t)中时间变量作用很大时，式(6) 很难保证成立，但式(5) 则没有此条件的限制。

其次，若假设2成立，则选定一个确定的递增函数L∈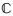^∞( $\mathbb{R}$ ₊; $\mathbb{R}$ ₊)，满足式(7)~(9)：

$ \mathop {\lim }\limits_{t \to \infty } L'\left( t \right)/{L^2}\left( t \right) = 0 $

(7)

$ \mathop {\lim }\limits_{t \to \infty } \left( {h\left( t \right) + \ln t} \right)/L\left( t \right) = 0 $

(8)

$ L\left( t \right) \ge \ln \lambda \left( t \right),\forall t \ge 0 $

(9)

由文献[9]可知，满足条件(7)~(9) 的L(t)总是存在的；另外，由式(9) 可知， $\mathop {\lim L}\limits_{t \to + \infty } $ (t)=+∞。

再次，选择两个局部Lipschitz连续的函数α, β∈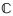( $\mathbb{R}$ ⁿ; $\mathbb{R}$ ₊)，使得式(10) 成立

$ \left\{ \begin{array}{l} \frac{{\alpha \left( \mathit{\boldsymbol{x}} \right)}}{{{\gamma ^{\frac{1}{2}}}\left( \mathit{\boldsymbol{x}} \right)}} \ge 0,\mathop {\lim }\limits_{\left| \mathit{\boldsymbol{x}} \right| \to + \infty } \frac{{\alpha \left( \mathit{\boldsymbol{x}} \right)}}{{{\gamma ^{\frac{1}{2}}}\left( \mathit{\boldsymbol{x}} \right)}} = + \infty ;\\ \frac{{\beta \left( \mathit{\boldsymbol{x}} \right)}}{{{\delta ^{\frac{1}{2}}}\left( \mathit{\boldsymbol{x}} \right)}} \ge 0,\mathop {\lim }\limits_{\left| \mathit{\boldsymbol{x}} \right| \to + \infty } \frac{{\beta \left( \mathit{\boldsymbol{x}} \right)}}{{{\delta ^{\frac{1}{2}}}\left( \mathit{\boldsymbol{x}} \right)}} = + \infty . \end{array} \right. $

(10)

最后，引入一个定义在(Ω, $\mathscr{F}$ , P)上的一维标准布朗运动B(t)，考虑如式(11) 的随机噪音项

$ \left( {L\left( t \right) + {h^{\frac{1}{2}}}\left( t \right)\left[ {\alpha \left( {\mathit{\boldsymbol{x}}\left( t \right)} \right) + \beta \left( {\mathit{\boldsymbol{x}}\left( {t - \tau } \right)} \right)} \right]} \right)\mathit{\boldsymbol{x}}\left( t \right){\rm{d}}B\left( t \right) $

(11)

进而得到随机时滞系统

$ \begin{array}{l} \;\;\;\;\;\;{\rm{d}}\mathit{\boldsymbol{x}}\left( t \right) = \left( {L\left( t \right) + {h^{\frac{1}{2}}}\left( t \right)\left[ {\alpha \left( {\mathit{\boldsymbol{x}}\left( t \right)} \right) + \beta \left( {\mathit{\boldsymbol{x}}\left( {t - } \right.} \right.} \right.} \right.\\ \left. {\left. {\left. {\left. \tau \right)} \right)} \right]} \right)\mathit{\boldsymbol{x}}\left( t \right){\rm{d}}B\left( t \right) + f\left( {\mathit{\boldsymbol{x}}\left( t \right),\mathit{\boldsymbol{x}}\left( {t - \tau } \right),t} \right){\rm{d}}t \end{array} $

(12)

2.2 解析解的存在唯一性

在研究解的稳定性问题之前，需要保证其整体解的存在唯一性。下面考虑式(12) 解的存在唯一性。

定理1 若假设1、2成立，则当式(10) 成立时，对初值ξ∈C([－τ, 0]; $\mathbb{R}$ ⁿ)，式(12) 存在唯一的整体解。

证明 由引理1可知，式(12) 在t∈[0, τ_e)有唯一强解，故只需说明τ_e=∞, a.s.；否则，对式(12) 的解x(t)，有P(τ_e＜+∞)>0成立。

定义如下停时

τ_k=inf{t∈[0, τ_e), |x(t)|≥k}

显然， $\mathop {\lim }\limits_{k \to \infty } $ τ_k≤τ_e, 从而存在充分小的ε∈(0, 1) 及充分大的N, T>0，对任意k≥N>0，有

$ P\left( {{\tau _k} < T} \right) \ge \varepsilon $

(13)

设ν∈(0, 1)，定义连续函数U(x)=|x|^ν，则由Ito公式可知，对任意k≥N，有

$ \begin{array}{l} \;\;\;\;\;\;\;U\left( {\mathit{\boldsymbol{x}}\left( {T \wedge {\tau _k}} \right)} \right) = {\left| {\xi \left( 0 \right)} \right|^\nu } + M\left( t \right) + \int_0^{T \wedge {\tau _k}} {LU} \\ \left( {\mathit{\boldsymbol{x}}\left( s \right),\mathit{\boldsymbol{x}}\left( {s - \tau } \right),s} \right){\rm{d}}s \end{array} $

其中

$ \begin{array}{l} \;\;\;\;\;\;\;LU\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}},s} \right) = \frac{\nu }{2}\left[ {2{{\left| \mathit{\boldsymbol{x}} \right|}^{\nu - 2}}{\mathit{\boldsymbol{x}}^{\rm{T}}}f\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}},s} \right) + \left( {\nu - 1} \right){{\left| \mathit{\boldsymbol{x}} \right|}^\nu }} \right.\\ \left. {{{\left( {L\left( s \right) + {h^{\frac{1}{2}}}\left( s \right)\alpha \left( \mathit{\boldsymbol{x}} \right) + {h^{\frac{1}{2}}}\left( s \right)\beta \left( \mathit{\boldsymbol{y}} \right)} \right)}^2}} \right] \end{array} $

$ \begin{array}{l} \;\;\;\;\;\;M\left( t \right) = \int_0^{T \wedge {\tau _k}} {\nu {{\left| {\left( \mathit{\boldsymbol{x}} \right)s} \right|}^{\nu - 1}}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( s \right)\left[ {L\left( s \right) + {h^{\frac{1}{2}}}\left( s \right)\alpha } \right.} \\ \left. {\left( {\mathit{\boldsymbol{x}}\left( s \right)} \right) + {h^{\frac{1}{2}}}\left( s \right)\beta \left( {\mathit{\boldsymbol{x}}\left( {s - \tau } \right)} \right)} \right]{\rm{d}}B\left( s \right) \end{array} $

显然，M(t)为连续局部鞅。

结合假设2和式(10)，对t≥0和x, y∈ $\mathbb{R}$ ⁿ，有

$ \begin{array}{l} LU\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}},s} \right) \le \frac{{\nu h\left( s \right)}}{2}{\left| \mathit{\boldsymbol{x}} \right|^\nu }\left( {2\theta \left[ {\gamma \left( \mathit{\boldsymbol{x}} \right) + \delta \left( \mathit{\boldsymbol{y}} \right)} \right] + } \right.\\ \left. {\left( {\nu - 1} \right)\left[ {{\alpha ^2}\left( \mathit{\boldsymbol{x}} \right) + {\beta ^2}\left( \mathit{\boldsymbol{y}} \right)} \right]} \right) \le \frac{{\nu h\left( s \right)}}{2}{\left| \mathit{\boldsymbol{x}} \right|^\nu }\left( {\gamma \left( \mathit{\boldsymbol{x}} \right)\left[ {2\theta + } \right.} \right.\\ \left. {\left. {\left( {\nu - 1} \right)\rho _1^2\left( \mathit{\boldsymbol{x}} \right)} \right] + \delta \left( \mathit{\boldsymbol{y}} \right)\left[ {2\theta + \left( {v - 1} \right)\rho _2^2\left( \mathit{\boldsymbol{y}} \right)} \right]} \right) \end{array} $

其中

$ {\rho _1}\left( \mathit{\boldsymbol{x}} \right): = \frac{{\alpha \left( \mathit{\boldsymbol{x}} \right)}}{{{\gamma ^{\frac{1}{2}}}\left( \mathit{\boldsymbol{x}} \right)}},{\rho _2}\left( \mathit{\boldsymbol{y}} \right): = \frac{{\beta \left( \mathit{\boldsymbol{y}} \right)}}{{{\delta ^{\frac{1}{2}}}\left( \mathit{\boldsymbol{y}} \right)}} $

显然有 $\mathop {\lim }\limits_{\left| \mathit{\boldsymbol{x}} \right| \to + \infty } $ ρ_i(x)=+∞, i=1, 2，则存在足够大的r₁, r₂>0，使得|x|≥r₁, |y|≥r₂时，有

$ \rho _1^2\left( \mathit{\boldsymbol{x}} \right) \ge \frac{{2\theta }}{{1 - \nu }},\rho _2^2\left( \mathit{\boldsymbol{y}} \right) \ge \frac{{2\theta }}{{1 - \nu }} $

再结合ν∈(0, 1)，可知

$ \mathop {\sup }\limits_{\left| \mathit{\boldsymbol{x}} \right| > {r_1},\left| \mathit{\boldsymbol{y}} \right| > {r_2}} LU\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}},s} \right) \le 0 $

故对任意的x、y，有

$ \begin{array}{l} \;\;\;\;\;\;LU\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}},s} \right) = \mathop {\sup }\limits_{\left| \mathit{\boldsymbol{x}} \right| \le {r_1},\left| \mathit{\boldsymbol{y}} \right| \le {r_2}} {\left| \mathit{\boldsymbol{x}} \right|^\nu }\left\{ {\gamma \left( \mathit{\boldsymbol{x}} \right)\left[ {2\theta + \left( {\nu - } \right.} \right.} \right.\\ \left. {\left. {\left. 1 \right)\rho _1^2\left( \mathit{\boldsymbol{x}} \right)} \right] + \delta \left( \mathit{\boldsymbol{y}} \right)\left[ {2\theta + \left( {v - 1} \right)\rho _2^2\left( \mathit{\boldsymbol{y}} \right)} \right]} \right\}\frac{{\nu h\left( s \right)}}{2} = :\\ Ch\left( s \right) \end{array} $

其中C为仅与r₁, r₂有关的正常数。从而有LU(x(s), x(s－τ), s)≤Ch(s)，对任意k≥N>0，有

$ \begin{array}{l} \;\;\;\;\;\;E\left( {{{\left| {\mathit{\boldsymbol{x}}\left( {T \wedge {\tau _k}} \right)} \right|}^\nu }} \right) \le {\left| {\xi \left( 0 \right)} \right|^\nu } + C\int_0^{T \wedge {\tau _k}} {h\left( s \right){\rm{d}}s} \le \\ {\left| {\xi \left( 0 \right)} \right|^\nu } + C\int_0^T {h\left( s \right){\rm{d}}s} < + \infty \end{array} $

(14)

然而，由式(13) 可知，对任意的k≥N，有E(|x(T∧τ_k)|^ν)≥k^νP(τ_k≤T)≥k^νε，即

$ \mathop {\lim }\limits_{k \to \infty } E{\left| {\mathit{\boldsymbol{x}}\left( {T \wedge {\tau _k}} \right)} \right|^\nu } = \infty $

(15)

显然，式(15) 与式(14) 相矛盾，因此对任意初值，有P(τ_e＜+∞)=0。证毕。

2.3 解析解的几乎处处渐近稳定性

下面考虑随机时滞系统式(12) 的稳定性。

定理2 若假设1、2成立，则当式(10) 成立时，对任意初值ξ∈C([－τ, 0]; $\mathbb{R}$ ⁿ)，式(12) 在t∈[0, +∞)上的解x(t)以一般衰减速度λ(t)几乎处处稳定，即

$ \mathop {\lim }\limits_{t \to \infty } \sup \frac{{\ln \left| {\mathit{\boldsymbol{x}}\left( t \right)} \right|}}{{\ln \lambda \left( t \right)}} < 0\;{\rm{a}}{\rm{.}}\;{\rm{s}}.。$

证明由Ito公式可得

$ \ln {\left| {\mathit{\boldsymbol{x}}\left( t \right)} \right|^2} = \ln {\left| {\xi \left( 0 \right)} \right|^2} + M\left( t \right) + \int_0^t {LU\left( {\mathit{\boldsymbol{x}}\left( s \right),\mathit{\boldsymbol{x}}\left( {s - \tau } \right),s} \right){\rm{d}}s} $

其中

$ \begin{array}{l} \;\;\;\;\;\;LU\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}},s} \right) = 2{\left| \mathit{\boldsymbol{x}} \right|^{ - 2}}{\mathit{\boldsymbol{x}}^{\rm{T}}}f\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}},s} \right) - \left[ {L\left( s \right) + {h^{\frac{1}{2}}}} \right.\\ {\left. {\left( s \right)\left( {\alpha \left( \mathit{\boldsymbol{x}} \right) + \beta \left( \mathit{\boldsymbol{y}} \right)} \right)} \right]^2} \end{array} $

$ \begin{array}{l} \;\;\;\;\;M\left( t \right): = 2\int_0^t {\left( {L\left( s \right) + h{{\left( s \right)}^{\frac{1}{2}}}\left( {\alpha \left( {\mathit{\boldsymbol{x}}\left( s \right)} \right) + \beta \left( \mathit{\boldsymbol{x}} \right.} \right.} \right.} \\ \left. {\left. {\left( {s - \tau } \right)} \right)} \right){\rm{d}}B\left( s \right) \end{array} $

显然M(t)为局部鞅。由指数鞅不等式^[3]可知，对任意ε∈ $\left( {0,\frac{1}{2}} \right)$ , k≥2, 有

$ P\left( {\mathop {\sup }\limits_{0 \le t \le k} M\left( t \right) - \frac{\varepsilon }{2}{{\left\langle M \right\rangle }_t} > \frac{2}{\varepsilon }\ln \left( {k - 1} \right)} \right) \le \frac{1}{{{{\left( {k - 1} \right)}^2}}} $

其中

$ \begin{array}{l} \;\;\;\;\;\;{\left\langle M \right\rangle _t} = 4\int_0^t {\left( {L\left( s \right) + h{{\left( s \right)}^{\frac{1}{2}}}\left( {\alpha \left( {\mathit{\boldsymbol{x}}\left( s \right)} \right) + \beta \left( \mathit{\boldsymbol{x}} \right.} \right.} \right.} \\ {\left. {\left. {\left( {s - \tau } \right)} \right)} \right)^2}{\rm{d}}s \end{array} $

表示M(t)的二次变差过程。

易知 $\sum\limits_{k = 1}^\infty {\frac{1}{{{{\left( {k - 1} \right)}^2}}}} $ ＜∞，故由Borel-Cantelli引理知，对几乎处处的ω∈Ω, 存在k₀=k₀(ω)，当k≥k₀时，有

$ \begin{array}{l} \;\;\;\;\;\;M\left( t \right) \le 2\varepsilon \int_0^t {\left( {L\left( s \right) + {h^{\frac{1}{2}}}\left( s \right)\left( {\alpha \left( {\mathit{\boldsymbol{x}}\left( s \right)} \right) + \beta \left( \mathit{\boldsymbol{x}} \right.} \right.} \right.} \\ {\left. {\left. {\left( {s - \tau } \right)} \right)} \right)^2}{\rm{d}}s + \frac{2}{\varepsilon }\ln k \end{array} $

从而有

$ \begin{array}{l} \;\;\;\;\;\;\;\;\ln {\left| {\mathit{\boldsymbol{x}}\left( t \right)} \right|^2} \le \ln {\left| {\xi \left( 0 \right)} \right|^2} + \frac{2}{\varepsilon }\ln k + \int_0^t {\left\{ {h\left( s \right)} \right.} \\ \left[ {\left( {2\theta \gamma \left( {\mathit{\boldsymbol{x}}\left( s \right)} \right) + \left( {2\varepsilon - 1} \right){\alpha ^2}\left( {\mathit{\boldsymbol{x}}\left( s \right)} \right)} \right) + \left( {2\theta \delta \left( {\mathit{\boldsymbol{x}}\left( {s - } \right.} \right.} \right.} \right.\\ \left. {\left. {\left. {\left. {\left. \tau \right)} \right) + \left( {2\varepsilon - 1} \right){\beta ^2}\left( {x\left( {s - \tau } \right)} \right)} \right)} \right] + \left( {2\varepsilon - 1} \right){L^2}\left( s \right)} \right\}{\rm{d}}s \end{array} $

(16)

注意到ε∈ $\left( {0,\frac{1}{2}} \right)$ ，则由式(10) 可知，对任意x∈ $\mathbb{R}$ ⁿ, 有

$ \begin{array}{l} \;\;\;\;\;\;\;\;2\theta \gamma \left( \mathit{\boldsymbol{x}} \right) + \left( {2\varepsilon - 1} \right){\alpha ^2}\left( \mathit{\boldsymbol{x}} \right) \le \left( {2\theta + \left( {2\varepsilon - 1} \right)} \right.\\ \left. {\rho _1^2\left( \mathit{\boldsymbol{x}} \right)} \right)\gamma \left( \mathit{\boldsymbol{x}} \right), \end{array} $

其中ρ₁(x):= $\frac{{\alpha \left( \mathit{\boldsymbol{x}} \right)}}{{{\gamma ^{\frac{1}{2}}}\left( \mathit{\boldsymbol{x}} \right)}}$ 。

又 $\mathop {\lim }\limits_{\left| \mathit{\boldsymbol{x}} \right| \to + \infty } $ ρ₁(x)=+∞，则存在足够大的N>0，使得

$ \rho _1^2\left( \mathit{\boldsymbol{x}} \right) \ge \frac{{2\theta }}{{1 - 2\varepsilon }},\forall \left| \mathit{\boldsymbol{x}} \right| \ge N $

进一步地，结合定理1中的证明可知

$ \mathop {\sup }\limits_\mathit{\boldsymbol{x}} \left( {2\theta \gamma \left( \mathit{\boldsymbol{x}} \right) + \left( {2\varepsilon - 1} \right){\alpha ^2}\left( \mathit{\boldsymbol{x}} \right)} \right) \le H\left( N \right) $

同理

$ \mathop {\sup }\limits_\mathit{\boldsymbol{y}} \left( {2\theta \delta \left( \mathit{\boldsymbol{y}} \right) + \left( {2\varepsilon - 1} \right){\beta ^2}\left( \mathit{\boldsymbol{y}} \right)} \right) \le M\left( N \right) $

其中H(N)、M(N)为仅依赖于N的正常数。因此，式(16) 有如下形式

$ \begin{array}{l} \;\;\;\;\;\;\ln {\left| {\mathit{\boldsymbol{x}}\left( t \right)} \right|^2} \le \int_0^t {\left( {h\left( s \right)\left( {M\left( N \right) + H\left( N \right)} \right) + } \right.} \\ \left. {\left( {2\varepsilon - 1} \right){L^2}\left( s \right)} \right){\rm{d}}s + \ln {\left| {\xi \left( 0 \right)} \right|^2} + \frac{2}{\varepsilon }\ln k \end{array} $

由式(7)、(8) 知，存在μ₁, μ₂>0，以及足够大的T＞0，使得对 $\forall $ t≥T, 有

$ \begin{array}{l} \;\;\;\;\;\;\;\left( {H\left( N \right) + M\left( N \right)} \right)h\left( t \right) + \left( {2\varepsilon - 1} \right){L^2}\left( t \right) \le \\ - {\mu _1}{L^2}\left( t \right) \le - {\mu _2}L'\left( t \right) \end{array} $

从而对任意的k≥max {k₀, T}和k－1≤t≤k，有

$ \begin{array}{l} \;\;\;\;\;\;\;\ln {\left| {\mathit{\boldsymbol{x}}\left( t \right)} \right|^2} \le \ln {\left| {\xi \left( 0 \right)} \right|^2} - \int_T^t {{\mu _2}L'\left( s \right){\rm{d}}s} + \frac{2}{\varepsilon }\\ \ln k + \int_0^T {\left( {h\left( s \right)\left( {M\left( N \right) + H\left( N \right)} \right) + \left( {2\varepsilon - 1} \right){L^2}\left( s \right)} \right)} \\ {\rm{d}}s \le - {\mu _2}L\left( t \right) + \frac{2}{\varepsilon }\ln k + C'\left( T \right) \end{array} $

其中

$ \begin{array}{l} \;\;\;\;\;C'\left( T \right) = \int_0^T {\left( {h\left( s \right)\left( {M\left( N \right) + H\left( N \right)} \right) + \left( {2\varepsilon - 1} \right)} \right.} \\ \left. {{L^2}\left( s \right)} \right){\rm{d}}s + \log {\left| {\xi \left( 0 \right)} \right|^2} + {\mu _2}L\left( T \right) \end{array} $

故

$ \frac{{\ln {{\left| {\mathit{\boldsymbol{x}}\left( t \right)} \right|}^2}}}{{L\left( t \right)}} \le \frac{{C'\left( T \right)}}{{L\left( t \right)}} - {\mu _2} + \frac{2}{{\varepsilon L\left( t \right)}}\ln \left( {t + 1} \right) $

再由式(9) 有

$ \mathop {\lim }\limits_{t \to + \infty } \frac{{\ln \left| {\mathit{\boldsymbol{x}}\left( t \right)} \right|}}{{\ln \lambda \left( t \right)}} \le \mathop {\lim }\limits_{t \to + \infty } \frac{{\ln \left| {\mathit{\boldsymbol{x}}\left( t \right)} \right|}}{{L\left( t \right)}} \le - \frac{{{\mu _2}}}{2}{\rm{a}}.\;{\rm{s}}. $

即非线性随机时滞系统式(12) 的精确解以一般衰减速度λ(t)几乎处处稳定(阶为 $\frac{{{\mu _2}}}{2}$ )。证毕。

3 实例分析

为了证明第2章随机时滞系统理论的有效性与正确性，本文通过一个实例进行验证。

考虑如下的一维非线性时滞系统

$ {\rm{d}}x\left( t \right) = x\left( t \right)\left[ {1 + {x^2}\left( {t - \tau } \right)} \right]{\rm{d}}t $

(17)

易知，式(17) 是不稳定的。

考虑加入合适的随机噪音进行干扰。

首先，不妨令θ=1，h(t)=1，γ(x)≡1，δ(y)=|y|²。由于此时f(x, y, t)=x(1+y²), 所以有xf(x, y, t)=x²(1+y²)=θh(t)(γ(t)+δ(y))x², 即假设2成立；

其次令L(t)=t，λ(t)=e^t，则

$ \mathop {\lim }\limits_{t \to \infty } L'\left( t \right)/{L^2}\left( t \right) = \mathop {\lim }\limits_{t \to \infty } \frac{1}{{{t^2}}} = 0, $

$ \begin{array}{l} \mathop {\lim }\limits_{t \to \infty } \left( {h\left( t \right) + \ln t} \right)/L\left( t \right) = \mathop {\lim }\limits_{t \to \infty } \frac{{1 + \ln t}}{t} = 0\;且\\ L\left( t \right) = t = {{\mathop{\rm lne}\nolimits} ^t} = \ln \lambda \left( t \right),\forall t \ge 0, \end{array} $

即式(7)~(9) 均成立；然后令α(x)=|x|, β(y)=|y|²，则

$ \frac{{\alpha \left( x \right)}}{{{\gamma ^{\frac{1}{2}}}\left( x \right)}} = \left| x \right| \to + \infty , $

同理

$ \frac{{\beta \left( y \right)}}{{{\delta ^{\frac{1}{2}}}\left( y \right)}} = \left| y \right| \to + \infty , $

从而式(10) 满足；

最后，得到如下的随机时滞系统

$ \begin{array}{l} \;\;\;\;\;{\rm{d}}x\left( t \right) = \left[ {t + \left| {x\left( t \right)} \right| + {x^2}\left( {t - \tau } \right)} \right]x\left( t \right){\rm{d}}B\left( t \right) + x\\ \left( t \right)\left( {1 + {x^2}\left( {t - \tau } \right)} \right){\rm{d}}t \end{array} $

(18)

易知，式(18) 漂移项与扩散项系数满足局部Lipschitz条件，即假设1成立；同时，它满足定理1和定理2的所有条件，故式(18) 存在唯一解，且该精确解几乎处处指数稳定。

4 结束语

本文研究非线性时滞系统式(4) 的随机稳定化问题，首先通过构造合适的扩散项系数，得到了相应的随机时滞微分系统式(12) 整体解的存在唯一性定理；进而利用指数鞅不等式等得到了其精确解以一般衰减速度的几乎处处稳定性，从而将文献[7]中得到的稳定化结果推广到时滞的情形；最后通过具体的实例分析，进一步证明了该理论的有效性。此外，与文献[5-6]相比，本文的漂移项系数f更加一般，且只需引入一个布朗运动随机项即可保证正则性和稳定性。