阴燃是多孔介质内的一种无焰放热燃烧反应,多孔介质的阴燃在垃圾焚烧和地下原油的提取方面有广泛应用,同时阴燃也是导致住宅火灾的主要原因,并破坏生物系统和土壤生态系统平衡。因此通过研究阴燃的数学性质认识阴燃发生发展的规律具有非常重要的意义。
根据阴燃波传播方向与来流空气方向的异同, 阴燃可分为正向阴燃和逆向阴燃。近些年来,国内外在阴燃问题的理论研究上大多数采用大活化能渐近分析法[1-6]。Schult等[5]利用大活化能渐近法找到两种具有不同结构的阴燃波的解,确定了阴燃的燃烧温度、传播速度和固体燃料的最终转化率的表达式;Wang等[6]利用渐近分析法研究水平方向的软质聚氨酯泡沫的阴燃传播,得到的分析结果与实验结果相符;Li等[7]利用数学分析的方法证明了绝热情形下无穷远处逆向阴燃波一维定常解的数学性质。但文献[5-6]所用方法较为复杂,且得到的表达式为近似解而非确定解;文献[7]主要对绝热情况下一维定常解的数学性质进行理论证明,而未考虑非绝热情况。基于目前研究中存在的这些问题,本文利用数学分析的方法研究非绝热情形下一维逆向阴燃波的定常解的数学性质,从理论上证明温度、固体质量浓度和氧气质量浓度在无穷远处的极限存在,并且利用Matlab进行数值模拟,使结果更加直观具体。
1 数学模型为避免次要因素使问题复杂化, 采用单步动力学反应机制:
| $ {\rm{A}} + \mu {{\rm{O}}_2} \to {\mu _{\rm{f}}}{\rm{B}} + {\mu _{\rm{g}}}{\rm{C}} + Q $ |
其中μ、μg和μf是基于质量的氧气、气体产物和固体产物的化学计量系数,A为燃料,B为固体产物,C为气体产物,Q为热量。
根据能量守恒、固体质量守恒和氧气质量浓度守恒,可以得到如式(1) 的控制方程[8]
| $ \left\{ \begin{array}{l} \frac{{\partial \theta }}{{\partial t}} + \frac{{\partial \theta }}{{\partial x}} = \frac{{{\partial ^2}\theta }}{{\partial {x^2}}} + \left( {y_{\rm{o}}^0 + \mu } \right)Da{Y_{\rm{f}}}{Y_{\rm{o}}}{{\rm{e}}^{ - {\theta _{\rm{a}}}/\theta }} - h\left( {\theta - {\theta _0}} \right)\\ \frac{{\partial {Y_{\rm{f}}}}}{{\partial t}} + {r_{\rm{f}}}\frac{{\partial {Y_{\rm{f}}}}}{{\partial x}} = - y_{\rm{o}}^0Da{Y_{\rm{f}}}{Y_{\rm{o}}}{{\rm{e}}^{ - {\theta _{\rm{a}}}/\theta }}\\ r\frac{{\partial {Y_{\rm{o}}}}}{{\partial t}} + {r_{\rm{g}}}\frac{{\partial {Y_{\rm{o}}}}}{{\partial x}} = \frac{1}{{Le}}\frac{{{\partial ^2}{Y_{\rm{o}}}}}{{\partial {x^2}}} - \mu Da{Y_{\rm{f}}}{Y_{\rm{o}}}{{\rm{e}}^{ - {\theta _{\rm{a}}}/\theta }} \end{array} \right. $ | (1) |
其中,x为空间变量,t为时间;θ、Yf和Yo分别为无量纲化的温度、固体反应物质量分数和氧气在气体中的质量浓度,yo0为无穷远处氧的质量浓度;θa为反应活化温度,θ0为无穷远处的环境温度;rf=Mf/M, rg=Mg/M,M=Mf+Mg(其中Mg和Mf分别为气体和固体的质量流量);r=ρg/ρf(其中ρg和ρf分别为气体密度和固体密度);Da=λB/cM2为Damköhler数,Le=λ/ρgcDa为Lewis数;λ为热传导系数,B为反应常数,c为固体与气体的比热容;h为热损失系数,h=0表示热损失为0,即为绝热情况,不同的h表示不同大小的对流热损失。
方程组(1) 的边界条件[8]为
| $ \left\{ \begin{array}{l} x \to - \infty :\frac{{{\rm{d}}\theta }}{{{\rm{d}}x}} = 0,\frac{{{\rm{d}}{Y_{\rm{f}}}}}{{{\rm{d}}x}} = 0,\frac{{{\rm{d}}{Y_{\rm{o}}}}}{{{\rm{d}}x}} = 0\\ x \to + \infty :\frac{{{\rm{d}}\theta }}{{{\rm{d}}x}} = 0,\frac{{{\rm{d}}{Y_{\rm{o}}}}}{{{\rm{d}}x}} = 0 \end{array} \right. $ | (2) |
式(2) 较文献[8]中少了一个边界条件
假定(θ*(x), Yf*(x), Yo*(x))是方程组(1) 的定常解,则它满足方程组(3)
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}{\theta ^ * }}}{{{\rm{d}}x}} - \frac{{{{\rm{d}}^2}{\theta ^ * }}}{{{\rm{d}}{x^2}}} = \left( {y_{\rm{o}}^0 + \mu } \right)DaY_{\rm{f}}^ * Y_{\rm{o}}^ * {{\rm{e}}^{ - {\theta _{\rm{a}}}/{\theta ^ * }}} - h\left( {{\theta ^ * } - {\theta _0}} \right)\\ {r_{\rm{f}}}\frac{{{\rm{d}}Y_{\rm{f}}^ * }}{{{\rm{d}}x}} = - y_{\rm{o}}^0DaY_{\rm{f}}^ * Y_{\rm{o}}^ * {{\rm{e}}^{ - {\theta _{\rm{a}}}/{\theta ^ * }}}\\ {r_{\rm{g}}}\frac{{{\rm{d}}Y_{\rm{o}}^ * }}{{{\rm{d}}x}} - \frac{1}{{Le}}\frac{{{\partial ^2}Y_{\rm{o}}^ * }}{{\partial {x^2}}} = - \mu DaY_{\rm{f}}^ * Y_{\rm{o}}^ * {{\rm{e}}^{ - {\theta _{\rm{a}}}/{\theta ^ * }}} \end{array} \right. $ | (3) |
式(3) 的边界条件为
| $ \left\{ \begin{array}{l} x \to - \infty :\frac{{{\rm{d}}{\theta ^ * }}}{{{\rm{d}}x}} = 0,\frac{{{\rm{d}}Y_{\rm{f}}^ * }}{{{\rm{d}}x}} = 0,\frac{{{\rm{d}}Y_{\rm{o}}^ * }}{{{\rm{d}}x}} = 0\\ x \to + \infty :\frac{{{\rm{d}}{\theta ^ * }}}{{{\rm{d}}x}} = 0,\frac{{{\rm{d}}Y_{\rm{o}}^ * }}{{{\rm{d}}x}} = 0 \end{array} \right. $ | (4) |
定理1 假设(θ*(x), Yf*(x), Yo*(x))是方程组(3) 满足式(4) 的解,则
证明 由方程组(3) 中第二个方程得
假设
| $ \mathop {\lim }\limits_{x \to + \infty } \left( {{r_{\rm{g}}}Y_{\rm{o}}^ * - \frac{1}{{Le}}\frac{{{\rm{d}}Y_{\rm{o}}^ * }}{{{\rm{d}}x}}} \right) = - \infty $ |
又由边界条件
证毕。
引理1 假设(θ*(x), Yf*(x), Yo*(x))是方程组(3) 满足式(4) 的充分光滑的解,则
证明 由方程组(3) 的第二个方程可得
| $ \begin{array}{l} \;\;\;\;\;\;\;{r_{\rm{f}}}\frac{{{{\rm{d}}^2}Y_{\rm{f}}^ * }}{{{\rm{d}}{x^2}}} = - y_{\rm{o}}^0Da\left( {Y_{\rm{o}}^ * {{\rm{e}}^{ - {\theta _{\rm{a}}}/{\theta ^ * }}}\frac{{{\rm{d}}Y_{\rm{f}}^ * }}{{{\rm{d}}x}} + Y_{\rm{f}}^ * {{\rm{e}}^{ - {\theta _{\rm{a}}}/{\theta ^ * }}}} \right.\\ \left. {\frac{{{\rm{d}}Y_{\rm{o}}^ * }}{{{\rm{d}}x}} + Y_{\rm{f}}^ * Y_{\rm{o}}^ * {{\rm{e}}^{ - {\theta _{\rm{a}}}/{\theta ^ * }}}\frac{{{\theta _{\rm{a}}}}}{{{{\left( {{\theta ^ * }} \right)}^2}}}\frac{{{\rm{d}}{\theta ^ * }}}{{{\rm{d}}x}}} \right) \end{array} $ |
由定理1知Yf*、Yo*在[0, +∞)上有界,又θa、θ*均为正数,所以e-θa/θ*在[0, +∞)有界恒成立;结合方程组(3) 的第二个方程可得
| $ \mathop {\lim }\limits_{x \to + \infty } \frac{{{\rm{d}}{\theta ^ * }}}{{{\rm{d}}x}} = 0\;和\;\mathop {\lim }\limits_{x \to + \infty } \frac{{{\rm{d}}Y_{\rm{o}}^ * }}{{{\rm{d}}x}} = 0 $ |
得
以下证明
若
| $ \mathop {\lim }\limits_{n \to \infty } \frac{{{\theta _{\rm{a}}}}}{{{{\left( {{\theta ^ * }\left( {{x_n}} \right)} \right)}^2}}}{{\rm{e}}^{ - {\theta _{\rm{a}}}/{\theta ^ * }\left( {{x_n}} \right)}} = + \infty $ |
由于e-θa/θ*(xn)有界,故
证毕。
定理2 假设(θ*(x), Yf*(x), Yo*(x))是方程组(3) 满足式(4) 的解,且Yf*存在二阶偏导,则
证明 由
|Yf*(x2)-Yf*(x1)|<ε
所以对
| $ \bar M = \mathop {\sup }\limits_{x,t \in \left( {M, + \infty } \right)} \left| {Y_{\rm{f}}^ * \left( {x + t} \right) - Y_{\rm{f}}^ * \left( x \right)} \right| $ |
则有M≤ε;另由引理1得,存在常数M0使|Yf*″(x)|≤M0,则由Taylor公式得
| $ Y_{\rm{f}}^ * \left( {x + t} \right) = Y_{\rm{f}}^ * \left( x \right) + Y_{\rm{f}}^{ * '}\left( x \right)t + \frac{{Y_{\rm{f}}^{ * ''}\left( \xi \right)}}{2}{t^2},\xi \in \left( {x,x + t} \right) $ |
所以
| $ \left| {Y_{\rm{f}}^{ * '}\left( x \right)} \right| \le \frac{{\left| {Y_{\rm{f}}^ * \left( {x + t} \right) - Y_{\rm{f}}^ * \left( x \right)} \right|}}{t} + \frac{{\left| {Y_{\rm{f}}^{ * ''}\left( \xi \right)} \right|}}{2}t \le \frac{\varepsilon }{t} + \frac{{{M_0}}}{2}t $ |
取
| $ \left| {Y_{\rm{f}}^{ * '}} \right| \le \frac{3}{2}\sqrt {{M_0}\varepsilon } $ |
由ε的任意性知
证毕。
定理3 设(θ*(x), Yf*(x), Yo*(x))满足方程组(3) 和式(4),且θ*(x)有连续的3阶导数,则
| $ \mathop {\lim }\limits_{x \to + \infty } \frac{{{\rm{d}}Y_{\rm{f}}^ * }}{{{\rm{d}}x}} = 0。$ |
证明 首先证明其必要性。
由
| $ \mathop {\lim }\limits_{x \to + \infty } \frac{{{\rm{d}}Y_{\rm{f}}^ * }}{{{\rm{d}}x}} = a < 0 $ |
则存在M>0,对任意x>M,有
| $ \frac{{{\rm{d}}Y_{\rm{f}}^ * }}{{{\rm{d}}x}} < \frac{a}{2} $ |
将此不等式在[M, u]上积分有
| $ Y_{\rm{f}}^ * \left( u \right) \le Y_{\rm{f}}^ * \left( M \right) + \frac{a}{2}\left( {u - M} \right) $ |
因为a<0,所以
| $ \mathop {\lim }\limits_{u \to + \infty } Y_{\rm{f}}^ * \left( u \right) = - \infty $ |
这与
再证明其充分性。
由方程组(3) 的第二个方程及
| $ \mathop {\lim }\limits_{x \to + \infty } Y_{\rm{f}}^ * Y_{\rm{o}}^ * {{\rm{e}}^{ - {\theta _{\rm{a}}}/{\theta ^ * }}} = 0 $ |
再根据方程组(3) 的第一个方程及
| $ \mathop {\lim }\limits_{x \to + \infty } \left( {h{\theta ^ * } - \frac{{{{\rm{d}}^2}{\theta ^ * }}}{{{\rm{d}}{x^2}}}} \right) = h{\theta _0} $ |
即
对方程组(3) 第一个式子两边求导可得
| $ \frac{{{{\rm{d}}^3}{\theta ^ * }}}{{{\rm{d}}{x^3}}} = \frac{{{{\rm{d}}^2}{\theta ^ * }}}{{{\rm{d}}{x^2}}} - \frac{{\rm{d}}}{{{\rm{d}}x}}\left[ {\left( {y_{\rm{o}}^0 + \mu } \right)DaY_{\rm{f}}^ * Y_{\rm{o}}^ * {{\rm{e}}^{ - {\theta _{\rm{a}}}/{\theta ^ * }}}} \right] + h\frac{{{\rm{d}}{\theta ^ * }}}{{{\rm{d}}x}} $ | (5) |
将式(5) 右端第二项展开得
| $ \begin{array}{l} \;\;\;\;\;\;\;\left( {y_{\rm{o}}^0 + \mu } \right)Da\left( {Y_{\rm{o}}^ * {{\rm{e}}^{ - {\theta _{\rm{a}}}/{\theta ^ * }}}\frac{{{\rm{d}}Y_{\rm{f}}^ * }}{{{\rm{d}}x}} + Y_{\rm{f}}^ * {{\rm{e}}^{ - {\theta _{\rm{a}}}/{\theta ^ * }}}\frac{{{\rm{d}}Y_{\rm{o}}^ * }}{{{\rm{d}}x}} + } \right.\\ \left. {Y_{\rm{f}}^ * Y_{\rm{o}}^ * {{\rm{e}}^{ - {\theta _{\rm{a}}}/{\theta ^ * }}}\frac{{{\theta _{\rm{a}}}}}{{{{\left( {{\theta ^ * }} \right)}^2}}}\frac{{{\rm{d}}{\theta ^ * }}}{{{\rm{d}}x}}} \right) \end{array} $ | (6) |
由引理1的证明可知式(6) 有界,即式(5) 右端第二项有界;又由
| $ \mathop {\lim }\limits_{x \to + \infty } Y_{\rm{f}}^ * Y_{\rm{o}}^ * {{\rm{e}}^{ - {\theta _{\rm{a}}}/{\theta ^ * }}} = 0 $ |
可知Yf*Yo*e-θa/θ*在[0, +∞)上有界,由
结合
| $ \mathop {\lim }\limits_{x \to + \infty } \frac{{{{\rm{d}}^2}{\theta ^ * }}}{{{\rm{d}}{x^2}}} = 0 $ |
从而由方程组(3) 的第一个方程可知
证毕。
推论 由定理3可得,当环境温度θ0不为零时有
| $ \mathop {\lim }\limits_{x \to + \infty } Y_{\rm{f}}^ * \mathop {\lim }\limits_{x \to + \infty } Y_{\rm{o}}^ * = 0。$ |
为了说明理论推导的可靠性,利用Matlab进行数值模拟来验证理论证明的结果。采用配置法结合Lobatto ⅢA公式来求解方程,即先用配置法找到包含配置解的配置方程,然后用Lobatto ⅢA公式迭代求解该配置方程。迭代所需初始近似解采用去掉非线性项求解线性常微分方程得到,即去掉方程(3) 中非线性项,结合边界条件(4),求得线性常微分方程组的解为:
| $ \left\{ \begin{array}{l} \theta = {\theta ^0} + \left( {{\theta ^ * } - {\theta ^0}} \right){{\rm{e}}^x}\\ {Y_{\rm{f}}} = 1\\ {Y_{\rm{o}}} = 1 + \left( {Y_{\rm{o}}^ * - 1} \right){{\rm{e}}^r}{g^{Lex}} \end{array} \right.\;\;\;\;x \le 0 $ |
| $ \left\{ \begin{array}{l} \theta = {\theta ^ * }\\ {Y_{\rm{f}}} = Y_{\rm{f}}^{\rm{b}}\\ {Y_{\rm{o}}} = Y_{\rm{o}}^ * \end{array} \right.\;\;\;\;\;x > 0 $ | (7) |
其中θ*、Yo*分别为θ、Yo在x=0处的值,Yfb表示Yf在正无穷远处的值。θ*、Yo*和Yfb可利用大活化能渐进分析法求得[5]。
考虑富燃情况,数值计算中参数取值来自文献[6]。由式(7) 迭代到的相对误差小于10-5的数值结果如图 1~3所示。
|
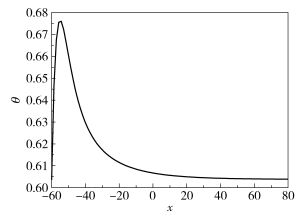
图 1 温度变化曲线 Fig.1 Temperature plot |
|
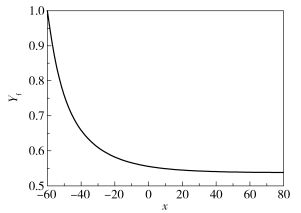
图 2 固体质量浓度变化曲线 Fig.2 Solid mass concentration plot |
|
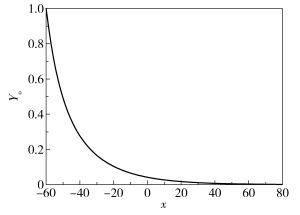
图 3 氧气质量浓度变化曲线 Fig.3 Oxygen concentration plot |
由图 1~3可知,在非绝热情形下温度、固体质量浓度和氧气质量浓度在无穷远处的极限仍然存在,且温度在无穷远处的极限为周围环境的室温,氧气质量浓度在富燃情形下趋于零。这与理论证明的结果相符合,说明计算结果具有一定的可靠性。
4 结论本文利用数学分析的方法研究了非绝热逆向阴燃波的一维定常解的数学性质。从理论上证明了温度、固体质量浓度和氧气质量浓度在空间变量趋于无穷时的极限存在,即
| [1] |
Dosanjh S S, Pagni P J, Fernandez-Pello A C. Forced cocurrent smoldering combustion[J]. Combustion and Flame, 1987, 68(2): 131-142. DOI:10.1016/0010-2180(87)90052-6 |
| [2] |
Lozinski D, Buckmaster J. The fast-time stability of a simple deflagration[J]. Combustion Science and Technology, 1995, 110/111(1): 379-391. DOI:10.1080/00102209508951932 |
| [3] |
Takashi K, Hidesaburo N. Global kinetic constants for thermal oxidative degradation of a cellulosic paper[J]. Combustion and Flame, 1992, 88(3/4): 345-368. |
| [4] |
Roy N C, Hossain A, Nakamura Y. A universal model of opposed flow combustion of solid fuel over an inert porous medium[J]. Combustion and Flame, 2014, 161(6): 1645-1658. DOI:10.1016/j.combustflame.2013.11.025 |
| [5] |
Schult D A, Matkowsky B J, Volpert V A. Propagation and extinction of forced opposed flow smolder waves[J]. Combustion and Flame, 1995, 101(4): 471-490. DOI:10.1016/0010-2180(94)00239-O |
| [6] |
Wang J H, Chao C Y H, Kong W J. Experimental study and asymptotic analysis of horizontally forced forward smoldering combustion[J]. Combustion and Flame, 2003, 135(4): 405-419. DOI:10.1016/j.combustflame.2003.07.001 |
| [7] |
Li Q S, Xu L X. A mathematical approach to the property of one-dimensional steady solution of reverse smolder waves[J]. Acta Mathematicae Applicatae Sinica, English Series, 2017, 33(1): 201-206. DOI:10.1007/s10255-017-0651-8 |
| [8] |
Yuan F P, Lu Z B. Structure and stability of non-adiabatic reverse smolder waves[J]. Applied Mathematics and Mechanics (English Edition), 2013, 34(6): 657-668. DOI:10.1007/s10483-013-1698-8 |








