2. 对外经济贸易大学 金融学院, 北京 100029
2. School of Finance and Banking, University of International Business and Economics, Beijing 100029, China
投资组合优化问题一直都是金融管理和金融数学领域的研究热点之一。自从Markowitz提出均值-方差模型(MVM)以来,投资组合理论与实践均获得长足发展。然而,均值-方差模型中的诸多弊端使其在风险测度方面不够完善且效率较低。Philippatos等[1-2]另辟蹊径率先将信息熵作为风险测度工具构建了投资组合优化模型,研究结果凸显出信息熵在度量投资组合风险方面的优势。近年来,增值熵、模糊熵、Yager熵、混合熵等广义熵概念被发掘并应用于投资组合等金融学领域[3-11]。其中,Xu等[5]为了解决随机不确定和模糊不确定情形下的投资组合选择问题,采用混合熵度量证券风险,从而建立了λ均值-混合熵模型(MHEM),本课题组[10-11]基于混合熵和模糊熵研究了投资组合优化问题,但没有约束限制。因此本文在文献[10-11]工作的基础上引入Yager熵约束方法[12-14],构建基于方差和混合熵为风险测度指标的投资组合优化模型,并使用上海证券交易所数据将其与传统单一指标测度模型进行实证对比研究,以期通过引入Yager熵更好地发挥方差和混合熵在风险控制方面的作用,为寻找高效投资组合模型提供一种新的思路。
1 混合熵混合熵同时具有随机不确定和模糊不确定性,是研究随机模糊不确定情形下投资组合风险度量的有效工具,其定义如下[5, 10-11]。
假设存在集合U,其有n个可能的状态{q1, q2, …, qn},每种状态发生的概率为{p1, p2, …, pn},又假定这n个可能的状态对某种特征的归属度为{μ1, μ2, …, μn},则定义混合熵为Hh=
Yager[12]提出一种用于优化投资组合资金分配比例的熵来评价概率分布的不确定性;Wu等[13]给出了基于Yager熵的线性规划模型,进一步拓展了Yager熵的应用,模型形式如下:
| $\begin{array}{l} \min \;\sum\limits_{i = 1}^n {\left( {e_i^ + + e_i^ - } \right)} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{array}{*{20}{l}} {{w_i} - \frac{1}{n} - e_i^ + + e_i^ - = 0,e_i^ + \ge 0,e_i^ - \ge 0}\\ {\sum\limits_{i = 1}^n {{w_i} = 1,i = 1,2, \cdots ,n,{w_i} \in \left[ {0,1} \right]} } \end{array}} \right. \end{array}$ |
其中,ei+和ei-分别为模型引入的正负偏差变量,模型目标函数为资金分配权重与1/n的正负偏差变量之和。
2 基于Yager熵的方差混合熵投资组合模型在类似文献[10-11]中的假设条件下,可建立带有Yager熵约束的均值-方差-混合熵模型(MVHEM-Y)
maxE[r1x1+r2x2+…+rnxn]
minV[r1x1+r2x2+…+rnxn]
min
| ${\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{array}{*{20}{l}} {\sum\limits_{i = 1}^n {{x_i} = 1} }\\ {{x_1},{x_2}, \cdots ,{x_n} \ge 0}\\ {{x_i} - \frac{1}{n} - e_i^ + + e_i^ - = e_i^ + \ge 0,e_i^ - \ge 0}\\ {\sum\limits_{i = 1}^n {\left( {e_i^ + + e_i^ - } \right)} \le \theta } \end{array}} \right.$ |
其中,E[r1x1+r2x2+…+rnxn]表示投资组合的期望收益率,V[r1x1+r2x2+…+rnxn]表示投资组合的方差风险度量,Hhi为投资组合中第i只证券的混合熵,X=(x1, x2, …, xn)T为n只证券的资金分配比例,ri为第i只证券的投资收益率,θ为正负偏差变量总和上限,其大小表示资金分配离散率的约束程度。
为了便于比较,本文给出文献[10-11]中的一些投资组合优化模型,分别为均值-方差-混合熵模型(MVHEM)、均值-方差模型(MVM)和均值-混合熵模型(MHEM),均可利用Matlab中的遗传算法工具箱进行最优化求解。
MVHEM如式(1) 所示
maxE[r1x1+r2x2+…+rnxn]
minV[r1x1+r2x2+…+rnxn]
min
| ${\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{array}{*{20}{l}} {\sum\limits_{i = 1}^n {{x_i} = 1} }\\ {{x_1},{x_2}, \cdots ,{x_n} \ge 0} \end{array}} \right.$ | (1) |
MVM形式如式(2)
maxE[r1x1+r2x2+…+rnxn]
minV[r1x1+r2x2+…+rnxn]
| ${\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{array}{*{20}{l}} {\sum\limits_{i = 1}^n {{x_i} = 1} }\\ {{x_1},{x_2}, \cdots ,{x_n} \ge 0} \end{array}} \right.$ | (2) |
MHEM如式(3)
maxE[r1x1+r2x2+…+rnxn]
min
| ${\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{array}{*{20}{l}} {\sum\limits_{i = 1}^n {{x_i} = 1} }\\ {{x_1},{x_2}, \cdots ,{x_n} \ge 0} \end{array}} \right.$ | (3) |
本文随机选取10只上交所股票,收集从2013年1月21日至2013年12月31日的有效日交易数据,并计算得到该期间的日收益率。日交易数据主要包括:开盘价P1t,收盘价P2t,当日最高股价P3t以及当日最低股价P4t,t表示时间,天。将每只股票的日收益率设定为一个三角模糊数r′=(r′lt, r′et, r′ht),其中r′lt=
随后,以此3类收益率的极大、极小值为区间上、下限,将3个大区间各自均分为10个小区间,并分别设定每个小区间的中点dlm、dem和dhm(m=1, 2…, 10) 作为初始聚类点进行K均值聚类。在此基础上,建立一步转移矩阵P,通过求解x=Px得到马尔科夫链的稳定解x,由此得到证券的模糊收益率re=
| 下载CSV 表 1 上交所10只证券的期望收益率、方差和混合熵 Table 1 Expected yields, variance and hybrid entropy of ten securities in SSE |
表 1表明,如果分别以方差和混合熵作为风险度量标准,得出的风险排序是存在差异的。原因在于方差测度的是微观层面收益率偏离平均值的幅度,而熵测度的是宏观层面整体收益率分布偏离均值分布的程度。此外,方差风险测度是完全基于随机不确定性的,而混合熵测度是基于随机不确定性和模糊不确定性的一种综合不确定性风险度量指标。
4 基础模型及实证检验为了方便使用Matlab中的多目标遗传算法工具箱求解,对原目标函数进行等价变换。令
| $\begin{array}{l} X = \left\{ {\left. x \right|\sum\limits_{i = 1}^n {{x_i} = 1} ,{x_i} = 1,{x_i} \ge 0,i = 1, \cdots ,n} \right\};\\ {E^ + } = \mathop {\max E}\limits_{x \in X} \left( x \right),{E^ - } = \mathop {\min E}\limits_{x \in X} \left( x \right);\\ {V^ + } = \mathop {\max V}\limits_{x \in X} \left( x \right),{V^ - } = \mathop {\min V}\limits_{x \in X} \left( x \right);\\ {H^ + } = \mathop {\max H}\limits_{x \in X} \left( x \right),{H^ - } = \mathop {\min H}\limits_{x \in X} \left( x \right){\rm{。}} \end{array}$ |
进而构造新的多目标函数
| $\begin{array}{l} \max \frac{{M\left( x \right) - {M^ - }}}{{{M^ + } - {M^ - }}}\\ \max \frac{{V\left( x \right) - {V^ - }}}{{{V^ - } - {V^ + }}}\\ \max \frac{{H\left( x \right) - {H^ + }}}{{{H^ - } - {H^ + }}}\\ {\rm{s}}{\rm{.t}}{\rm{.}}\quad \sum\limits_{i = 1}^N {{x_i} = 1,{x_1},{x_2}, \cdots ,{x_n} \ge 0} \end{array}$ | (4) |
通过求解得到多个帕累托最优解,将其按照收益导向型(MVHEM-Y)和风险导向型(MVHEM-R)进行分类,并在每种类型中分别选取最优投资组合作为代表进行比较。其中风险导向型的特征是以低风险指标为关注焦点,而收益导向型则以高收益率为主要求解方向。同时,为了更好地验证MVM的实证效果,加入简单平均策略(1/N strategy)进行对比,表 2给出了不同模型的最优投资组合资金分配情况。
| 下载CSV 表 2 不同模型的最优投资组合资金分配比例 Table 2 The funds allocation of optimal portfolio based on different models |
从表 2中不难看出,对于模型MVHEM-Y和MVHEM-R,后者的资金分配比例相对更为分散,前者偏重于关注高收益,从而使资金分配过于集中;而MVM求解得到的最优组合更倾向于平均分配资金比例,这与部分学者“角点解”的研究结论相悖,原因可能在于样本中不存在一只或多只在收益或风险方面表现显著优越的股票;MHEM求解得出的最优投资组合同样出现了资金配比过度集中的现象,如对股票600150的资金分配达到了61.09%。单纯从资金分配角度来看,MVHEM-R与MVM最优投资组合比较相似,原因是MVHEM-R在涉及微观层面风险测度时方差起到了较强作用。
以表 2中不同模型的最优投资组合为基础,再利用2014年1月9日至2015年1月19日的有效交易数据进行实证检验,检验结果如图 1所示。
|
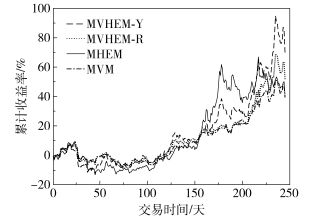
图 1 不同模型最优投资组合累计收益率 Fig.1 Accumulative yield performance of the optimal portfolio based on different models |
从图 1可以看到,表现最佳的两个投资组合是MVHEM-Y和MVHEM-R模型,前者的累计收益率更高,这符合收益导向的设定,但是波动也更大。整个实证期间基本可以分为前100天、100~220天以及最后30天3个阶段。前100天中,MVM以及MVHEM-R表现更好一些,MVHEM-Y和MHEM表现相对弱势;在100~220天内,情况完全反转,MVM以及MVHEM-R的走势比较接近,而MVHEM-Y和MHEM走势比较类似,尤其是第180天左右的急速拉升,使二者之间除了拉升幅度不同之外,走势基本吻合。值得注意的是,前期以方差为风险指标的MVM表现优秀,后期以混合熵为险度量的MHEM表现出色,MVHEM-Y和MVHEM-R的走势大部分时间段内是夹在中间的,原因可能方差和混合熵同时作为风险指标起到了一定的平衡作用。
以MVM模型与1/N策略的最优投资组合为基础,利用2014年1月9日至2015年1月19日的有效交易数据进行实证检验,检验结果如图 2所示。
|
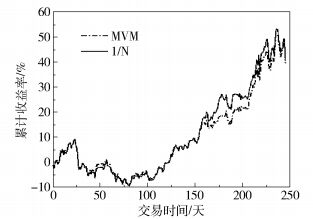
图 2 MVM模型与1/N策略最优投资组合累计收益率 Fig.2 Accumulative yield performance of the optimal portfolio based on MVM and 1/N strategy |
从图 2可以看到,MVM在前100天的累计收益率表现与平均分配策略几乎一致,但是之后的表现并不理想。值得注意的是,从长远的角度来看(以实证研究为观察区间),MVM最优投资组合的投资收益率甚至要低于简单的平均分配策略。
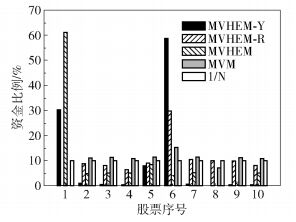
5 Yager熵约束下模型及实证检验尽管第4章中以方差-混合熵(VHE)为风险度量的模型MVHEM-Y和MVHEM-R实证表现优于其他传统模型,但从图 3来看,其资金分配出现了过于集中的现象,这有悖于分散投资风险的理念。为此,本文通过加入Yager熵约束对MVHEM-Y和MVHEM-R资金比例进行控制,求解得到加入Yager熵约束后的MVHEM-Y-Y与MVHEM-R-Y的资金比例分配情况,如图 4所示。
|
图 3 不同模型最优投资组资金分配比例 Fig.3 Funds allocation of optimal portfolio based on different models |
|
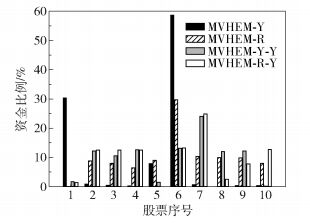
图 4 加入Yager熵约束后不同模型最优投资组合下的证券资金分配比例 Fig.4 Funds allocation of optimal portfolio based on different models with Yager's entropy |
从图 4可以看到,加入Yager熵约束后的均值-方差-混合熵模型(MVHEM-Y-Y)最优投资组合的资金分配比例有了显著的改善,特别是MVHEM-Y-Y,其权重集中的现象改善尤其明显,使得模型更加符合分散投资风险的理念。
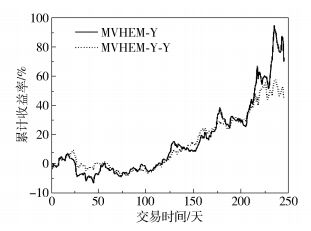
同样利用2014年1月9日至2015年1月19日的有效交易数据进行检验,结果如图 5所示。从图 5可以看出,MVHEM-Y-Y整体走势更加平稳,且在市场回调时仍能保持不错的抗风险能力,特别是在100~200天区间内,MVHEM-Y累计收益率曲线刚好围绕MVHEM-Y-Y进行波动;在后期,MVHEM-Y-Y走势基本与MVHEM-Y一致,只是波动幅度有所减小。
|
图 5 加入资金比例约束的收益导向混合熵模型累计收益率 Fig.5 Accumulative yield performance of the optimal portfolio based on MVHEM-Y and MVHEM-Y-Y |
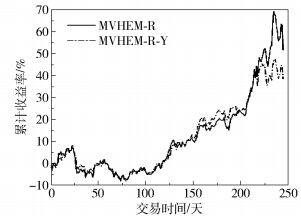
图 6为加入Yager熵前后风险导向型均值-方差-混合熵模型(MVHEM-R-Y)的累计收益率实证表现。值得关注的是,尽管资金分配比例有了巨大的变化,但二者的走势在前150天的实证区间内几乎是重合的,中后期MVHEM-R-Y较MVHEM-R走势也更加平稳;但是鉴于MVHEM-R最优投资组合本身的资金分配并没有过于集中,模型结果更加偏重于风险控制,因此,加入Yager熵后的效果没有收益导向模型显著,在最后的拉升中二者之间的走势基本相似,且MVHEM-R-Y在控制波动风险方面表现更佳。
|
图 6 加入资金比例约束的风险导向混合熵模型累计收益率 Fig.6 Accumulative yield performance of the optimal portfolio based on MVHEM-R and MVHEM-R-Y |
本文以方差和混合熵作为风险测度指标,引入可信性方法和Yager熵约束,同时对随机不确定性和模糊不确定性进行综合考量,并与其他模型进行实证比较。结果表明,相较其他传统模型,以方差-混合熵为风险度量的投资组合优化模型可以较好地均衡方差和混合熵在风险控制方面的作用,进一步增强模型的稳定性,在控制风险的情况下实现良好的累计收益率。对于当前金融环境复杂、多空力量交错、投机氛围浓厚环境下的证券投资行为,本文模型具有一定的指导作用和实用价值。
| [1] |
Philippatos G C, Wilson C J. Entropy, market risk and the selection of efficient portfolios:comment[J]. Applied Economics, 1972, 4(3): 209-220. DOI:10.1080/00036847200000017 |
| [2] |
Philippatos G C, Gressis N. Conditions of equivalence among E-V, SSD, and E-H portfolio selection criteria:the case for uniform, Normal and lognormal distributions[J]. Management Science, 1975, 21(6): 617-625. DOI:10.1287/mnsc.21.6.617 |
| [3] |
Ou J S. Theory of portfolio and risk based on incremental entropy[J]. Journal of Risk Finance, 2005, 6(1): 31-39. DOI:10.1108/15265940510574754 |
| [4] |
Huang X X. Mean-entropy models for fuzzy portfolio selection[J]. IEEE Transactions on Fuzzy Systems, 2008, 16(4): 1096-1101. DOI:10.1109/TFUZZ.2008.924200 |
| [5] |
Xu J P, Zhou X Y, Wu D D. Portfolio selection using λ mean and hybrid entropy[J]. Annals of Operations Research, 2011, 185(1): 213-229. DOI:10.1007/s10479-009-0550-3 |
| [6] |
Zhang W G, Liu Y J, Xu W J. A possibilistic mean-semivariance-entropy model for multi-period portfolio selection with transaction costs[J]. European Journal of Operational Research, 2012, 222(2): 341-349. DOI:10.1016/j.ejor.2012.04.023 |
| [7] |
Zhou R X, Cai R, Tong G Q. Applications of entropy in finance:a review[J]. Entropy, 2013, 15(11): 4909-4931. DOI:10.3390/e15114909 |
| [8] |
Backus D, Chernov M, Zin S. Sources of entropy in representative agent models[J]. Journal of Finance, 2014, 69(1): 51-99. DOI:10.1111/jofi.12090 |
| [9] |
Zhou R X, Yang Z B, Yu M, et al. A portfolio optimization model based on information entropy and fuzzy time series[J]. Fuzzy Optimization and Decision Making, 2015, 14(4): 381-397. DOI:10.1007/s10700-015-9206-8 |
| [10] |
Zhou R X, Zhan Y, Cai R, et al. A mean-variance hybrid-entropy model for portfolio selection with fuzzy returns[J]. Entropy, 2015, 17(5): 3319-3331. DOI:10.3390/e17053319 |
| [11] |
周荣喜, 王迪, 展宇, 等. 基于模糊熵和Yager熵的投资组合优化模型[J]. 北京化工大学学报:自然科学版, 2015, 42(5): 124-128. Zhou R X, Wang D, Zhan Y, et al. Portfolio optimization model based on fuzzy entropy and Yager's entropy[J]. Journal of Beijing University of Chemical Technology:Natural Science, 2015, 42(5): 124-158. (in Chinese) |
| [12] |
Yager R R. Measures of entropy and fuzziness related to aggregation operators[J]. Information Sciences, 1995, 82(3/4): 147-166. |
| [13] |
Wu J, Sun B L, Liang C Y, et al. A linear programming model for determining ordered weighted averaging operator weights with maximum Yager's entropy[J]. Computers & Industrial Engineering, 2009, 57(3): 742-747. |
| [14] |
董雪璠, 王秀国, 周荣喜, 等. 基于最小信息熵-最大增值熵的投资组合优化模型[J]. 北京化工大学学报:自然科学版, 2011, 38(6): 120-124. Dong X F, Wang X G, Zhou R X, et al. Portfolio optimization model based on the minimum comentropy and the maximum value-added entropy[J]. Journal of Beijing University of Chemical Technology:Natural Science, 2011, 38(6): 120-124. (in Chinese) |








