信息爆炸的时代,每时每刻都会产生海量的信息。为了更好地对海量数据进行挖掘和运用,需要先对数据进行预处理,即去除数据中的各种噪声,保留真实有效的数据。主成分分析(principal component analysis, PCA)[1]是一种非常经典的降维方法,在许多领域中被广泛应用。PCA常用奇异值分解算法来求解, 能有效去除数据中的稠密小噪声,实现降维的目的,但是当需要分离出数据中的稀疏大噪声时,PCA方法不再适用。鲁棒主成分分析(robust PCA,RPCA)[1-4]能有效分离出数据中的稀疏大噪声,目前一些主流算法,如迭代阈值算法(iterative thresholding, IT)[5], 加速的近端梯度算法(accelerated proximal gradient, APG) [6]和增广的拉格朗日乘子法(augmented Lagrange multiplier, ALM)[7]等能对其有效求解,但是这些算法都只能分离出其中的大噪声,而无法分离出稠密小噪声。
本文提出用随机排序的交替方向乘子法(randomly permuted ADMM, RP-ADMM)来求解更一般的RPCA模型(G-RPCA), 即在数据中同时存在稀疏大噪声和稠密小噪声的情形,同时证明了当RP-ADMM被应用到G-RPCA模型中时,结果是收敛的。
1 广义的鲁棒主成分分析及算法 1.1 广义的鲁棒主成分分析广义的鲁棒主成分分析(G-RPCA)是一种矩阵恢复模型,它能从含有混合噪声的高维数据矩阵中分离出稀疏大噪声和稠密小噪声,从而得到有价值的低维数据矩阵。G-RPCA能写成如下形式:
| $\left\{ {\begin{array}{*{20}{l}} {\mathop {{\rm{min}}}\limits_{A,E} {{\left\| \mathit{\boldsymbol{A}} \right\|}_*} + \lambda {{\left\| \mathit{\boldsymbol{E}} \right\|}_1} + \gamma \left\| \mathit{\boldsymbol{F}} \right\|_F^2}\\ {{\rm{subject to}}\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{E}} + \mathit{\boldsymbol{F}} = \mathit{\boldsymbol{D}}} \end{array}} \right.$ | (1) |
其中,‖·‖F2为F范数,表示稠密小噪声;‖·‖*为核范数,表示低秩矩阵;‖·‖1为1范数,表示稀疏大噪声。
1.2 随机排序的交替方向乘子法随机排序的交替方向乘子法是一种迭代方法,由交替方向乘子法(ADMM)[8]改进而来。ADMM适用的凸优化问题如式(2) 所示:
| $\left\{ {\begin{array}{*{20}{l}} {{\rm{min}}\;{f_1}({\mathit{\boldsymbol{x}}_1}) + {f_2}({\mathit{\boldsymbol{x}}_2})}\\ {{\rm{subject to}}{\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{A}}_2}{\mathit{\boldsymbol{x}}_2} = \mathit{\boldsymbol{b}}} \end{array}} \right.$ | (2) |
其中f1(x1)和f2(x2)是两个可分离的目标函数,A1x1+A2x2=b是一个线性约束条件[9]。
为了求解式(2) 需先写出其增广Lagrangian函数形式:
| $\begin{align} & \quad L({{\mathit{\boldsymbol{x}}}_{1}},{{\mathit{\boldsymbol{x}}}_{2}};\mu )={{f}_{1}}({{\mathit{\boldsymbol{x}}}_{1}})+{{f}_{2}}({{\mathit{\boldsymbol{x}}}_{2}})-\mu ({{\mathit{\boldsymbol{A}}}_{1}}{{\mathit{\boldsymbol{x}}}_{1}}+ \\ & {{\mathit{\boldsymbol{A}}}_{1}}{{\mathit{\boldsymbol{x}}}_{2}}-\mathit{\boldsymbol{b}})+\frac{\beta }{2}{{\left\| {{\mathit{\boldsymbol{A}}}_{1}}{{\mathit{\boldsymbol{x}}}_{1}}+{{\mathit{\boldsymbol{A}}}_{2}}{{\mathit{\boldsymbol{x}}}_{2}}-\mathit{\boldsymbol{b}} \right\|}^{2}} \\ \end{align}$ | (3) |
其中μ是Lagrangian乘子,β>0为惩罚因子。循环迭代更新原来的变量x1, x2
| $\left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{x}}_1^{k + 1} = \mathop {{\rm{argmin}}\;}\limits_{{x_1} \in {\chi _1}} L\left( {{\mathit{\boldsymbol{x}}_1},\mathit{\boldsymbol{x}}_2^k,{\mu ^k}} \right)}\\ {\mathit{\boldsymbol{x}}_2^{k + 1} = \mathop {{\rm{argmin}}\;}\limits_{{x_2} \in {\chi _2}} L\left( {{\mathit{\boldsymbol{x}}_2},\mathit{\boldsymbol{x}}_1^k,{\mu ^k}} \right)}\\ {{\mu ^{k + 1}} = {\mu ^k} - \beta ({\mathit{\boldsymbol{A}}_1}\mathit{\boldsymbol{x}}_1^{k + 1} + {\mathit{\boldsymbol{A}}_2}\mathit{\boldsymbol{x}}_2^{k + 1} - \mathit{\boldsymbol{b}})} \end{array}} \right.$ |
RP-ADMM算法考虑的是模型(2) 中目标函数为3个或3个以上时的情形,以3个为例:
| $\left\{ {\begin{array}{*{20}{l}} {{\rm{min}}\;{f_1}({\mathit{\boldsymbol{x}}_1}) + {f_2}({\mathit{\boldsymbol{x}}_2}) + {f_3}({\mathit{\boldsymbol{x}}_3})}\\ {{\rm{subject to}}{\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{A}}_2}{\mathit{\boldsymbol{x}}_2} + {\mathit{\boldsymbol{A}}_3}{\mathit{\boldsymbol{x}}_3} = \mathit{\boldsymbol{b}}} \end{array}} \right.$ | (4) |
将式(4) 写成增广Lagrangian函数的形式:
| $\begin{align} & \quad L({{\mathit{\boldsymbol{x}}}_{1}},{{\mathit{\boldsymbol{x}}}_{2}},{{\mathit{\boldsymbol{x}}}_{3}};\mu )={{f}_{1}}({{\mathit{\boldsymbol{x}}}_{1}})+{{f}_{2}}({{\mathit{\boldsymbol{x}}}_{2}})+{{f}_{3}}({{\mathit{\boldsymbol{x}}}_{3}})- \\ & \mu ({{\mathit{\boldsymbol{A}}}_{1}}{{\mathit{\boldsymbol{x}}}_{1}}+{{\mathit{\boldsymbol{A}}}_{1}}{{\mathit{\boldsymbol{x}}}_{2}}+{{\mathit{\boldsymbol{A}}}_{3}}{{\mathit{\boldsymbol{x}}}_{3}}-\mathit{\boldsymbol{b}})+\frac{\beta }{2}\left\| {{\mathit{\boldsymbol{A}}}_{1}}{{\mathit{\boldsymbol{x}}}_{1}}+{{\mathit{\boldsymbol{A}}}_{2}}{{\mathit{\boldsymbol{x}}}_{2}}+{{\mathit{\boldsymbol{A}}}_{3}}{{\mathit{\boldsymbol{x}}}_{3}}- \right. \\ & {{\left. \mathit{\boldsymbol{b}} \right\|}^{2}} \\ \end{align}$ | (5) |
RP-ADMM和ADMM的区别在于,RP-ADMM算法在每次迭代前都会随机抽取一个排序,例如:σ=(2, 3, 1),L(xσ(1), xσ(2), xσ(3); μ)=L(x2, x3, x1; μ)表示先固定x3, x1求解出x2,再固定x2, x1求解出x3,最后固定x2, x3求解出x1。
1.3 模型推导及算法流程为了求解G-RPCA模型的迭代过程,需要先将式(1) 写成增广Lagrangian函数的形式:
| $\begin{array}{l} \quad L\left( {\mathit{\boldsymbol{A}},\mathit{\boldsymbol{E}},\mathit{\boldsymbol{F}},\mathit{\boldsymbol{Y}},\mu } \right) = {\left\| \mathit{\boldsymbol{A}} \right\|_*} + \lambda {\left\| \mathit{\boldsymbol{E}} \right\|_1}\\ + \frac{\gamma }{2}\left\| \mathit{\boldsymbol{F}} \right\|_F^2 + \left\langle {\mathit{\boldsymbol{Y}},\mathit{\boldsymbol{D}} - \mathit{\boldsymbol{A}} - \mathit{\boldsymbol{E}} - \mathit{\boldsymbol{F}}} \right\rangle + \\ \frac{\mu }{2}\left\| {\mathit{\boldsymbol{D}} - \mathit{\boldsymbol{A}} - \mathit{\boldsymbol{E}} - \mathit{\boldsymbol{F}}} \right\|_F^2 \end{array}$ | (6) |
其中F为稠密的小噪声矩阵,‖·‖F为F范数。
根据式(6) 得到如下迭代格式的推导过程。
首先固定Ek和Fk,更新Ak+1:
| $\begin{array}{l} \quad {\rm{arg}}\mathop {{\rm{min}}}\limits_{{A_{k + 1}}} {\rm{}}{\left\| {{\mathit{\boldsymbol{A}}_{k + 1}}} \right\|_*} + \frac{\mu }{2}\left\| {\mathit{\boldsymbol{D}} - {\mathit{\boldsymbol{A}}_{k + 1}} - {\mathit{\boldsymbol{E}}_k} - {\mathit{\boldsymbol{F}}_k}\mathit{\boldsymbol{ + }}} \right.\\ \left. {\mu _k^{ - 1}{\mathit{\boldsymbol{Y}}_k}} \right\|_F^2 = {D_{\mu {k^{ - 1}}}}\left( {\mathit{\boldsymbol{D}} - {\mathit{\boldsymbol{E}}_k} - {\mathit{\boldsymbol{F}}_k}\mathit{\boldsymbol{ + }}\mu _k^{ - 1}{\mathit{\boldsymbol{Y}}_k}} \right) \end{array}$ | (7) |
其中,Dμk-1(·)=USμk-1(Σ)VT;对D-Ek-Fk+μk-1Yk进行奇异值分解得到矩阵U, Σ和V,Sμk-1(·)为收缩算子,
| ${S_{\mu {k^{ - 1}}}}\left( x \right) = \left\{ {\begin{array}{*{20}{l}} {x - \mu _k^{ - 1},} & {x > \mu _k^{ - 1}}\\ {x + \mu _k^{ - 1},} & {x < - \mu _k^{ - 1}}\\ {0,} & 其他 \end{array}} \right.$ |
其次固定Ak和Fk,更新Ek+1
| $\begin{array}{l} \quad {\rm{arg}}\mathop {{\rm{min}}}\limits_{{\mathit{\boldsymbol{E}}_{k + 1}}} {\rm{}}{\left\| {{\mathit{\boldsymbol{E}}_{k + 1}}} \right\|_*} + \frac{{{\mu _k}}}{2}\left\| {\mathit{\boldsymbol{D}} - {\mathit{\boldsymbol{A}}_k} - {\mathit{\boldsymbol{E}}_{k + 1}} - {\mathit{\boldsymbol{F}}_k}\mathit{\boldsymbol{ + }}} \right.\\ \left. {\mu _k^{ - 1}{\mathit{\boldsymbol{Y}}_k}} \right\|_F^2 = {S_{\frac{\lambda }{{\mu k}}}}\left( {\mathit{\boldsymbol{D}} - {\mathit{\boldsymbol{A}}_k} - {\mathit{\boldsymbol{F}}_k}\mathit{\boldsymbol{ + }}\mu _k^{ - 1}{\mathit{\boldsymbol{Y}}_k}} \right) \end{array}$ | (8) |
最后固定Ak和Ek更新Fk+1
| $\begin{array}{l} \quad {\rm{arg}}\mathop {{\rm{min}}}\limits_{{\mathit{\boldsymbol{F}}_{k + 1}}} {\rm{}}\frac{\gamma }{2}\left\| {{\mathit{\boldsymbol{F}}_{k + 1}}} \right\|_F^2 + \frac{\mu }{2}\left\| {\mathit{\boldsymbol{D}} - {\mathit{\boldsymbol{A}}_k} - {\mathit{\boldsymbol{E}}_k} - {\mathit{\boldsymbol{F}}_{k + 1}}\mathit{\boldsymbol{ + }}} \right.\\ \left. {\mu _k^{ - 1}{\mathit{\boldsymbol{Y}}_k}} \right\|_F^2 = \frac{{{\mu _k}}}{{{\mu _k} + \gamma }}\left( {\mathit{\boldsymbol{D}} - {\mathit{\boldsymbol{A}}_k} - {\mathit{\boldsymbol{E}}_k}\mathit{\boldsymbol{ + }}{\mu _k}{\mathit{\boldsymbol{Y}}_k}} \right) \end{array}$ | (9) |
由式(7)~(9) 并结合RP-ADMM得到如下G-RPCA的算法流程。
1) 输入数据矩阵D
2) 初始化
令Y0,μ0>0,ρ>0,γ=0.5,k=0, A0=0,E0=0,F0=0;
3) 产生一个(1, 2, 3) 的随机排序σ;
4) 遍历σ,如σ(i)=1,则转步骤5),如σ(i)=2,则转步骤6),如果σ(i)=3,则转步骤7);
5) 应用式(7) 得到Ak+1,令Ak=Ak+1;
6) 应用式(8) 得到Ek+1,令Ek=Ek+1;
7) 应用式(9) 得到Fk+1,令Fk=Fk+1;
8)Yk+1=Yk+μk(D-Ak-Ek-Fk),μk+1=ρμk,k=k+1;
9) 检查是否收敛,如不收敛转步骤3),收敛则输出。
10) 输出Ak*,Ek*,Fk*。
1.4 收敛性证明证明RP-ADMM算法的收敛性。
1) 利用ADMM对式(6) 进行k次迭代时有式(10) 成立:
| $\left\{ {\begin{array}{*{20}{l}} { - \mathit{\boldsymbol{a}}_1^{\rm{T}}{\mathit{\boldsymbol{\lambda }}^k} + \mathit{\boldsymbol{a}}_1^{\rm{T}}({\mathit{\boldsymbol{a}}_1}\mathit{\boldsymbol{x}}_1^{k + 1} + {\mathit{\boldsymbol{a}}_2}\mathit{\boldsymbol{x}}_2^k + {\mathit{\boldsymbol{a}}_3}\mathit{\boldsymbol{x}}_3^k - \mathit{\boldsymbol{b}}) = 0}\\ { - \mathit{\boldsymbol{a}}_2^{\rm{T}}{\mathit{\boldsymbol{\lambda }}^k} + \mathit{\boldsymbol{a}}_2^{\rm{T}}({\mathit{\boldsymbol{a}}_1}\mathit{\boldsymbol{x}}_1^{k + 1} + {\mathit{\boldsymbol{a}}_2}\mathit{\boldsymbol{x}}_2^{k + 1} + {\mathit{\boldsymbol{a}}_3}\mathit{\boldsymbol{x}}_3^k - \mathit{\boldsymbol{b}}) = 0}\\ { - \mathit{\boldsymbol{a}}_3^{\rm{T}}{\mathit{\boldsymbol{\lambda }}^k} + \mathit{\boldsymbol{a}}_3^{\rm{T}}({\mathit{\boldsymbol{a}}_1}\mathit{\boldsymbol{x}}_1^{k + 1} + {\mathit{\boldsymbol{a}}_2}\mathit{\boldsymbol{x}}_2^{k + 1} + {\mathit{\boldsymbol{a}}_3}\mathit{\boldsymbol{x}}_3^{k + 1} - \mathit{\boldsymbol{b}}) = 0}\\ {\left( {{\mathit{\boldsymbol{a}}_1}\mathit{\boldsymbol{x}}_1^{k + 1} + {\mathit{\boldsymbol{a}}_2}\mathit{\boldsymbol{x}}_2^{k + 1} + {\mathit{\boldsymbol{a}}_3}\mathit{\boldsymbol{x}}_3^{k + 1} - \mathit{\boldsymbol{b}}} \right) + {\mathit{\boldsymbol{\lambda }}^{k + 1}} - {\mathit{\boldsymbol{\lambda }}^k} = 0} \end{array}} \right.$ | (10) |
其中λ表示拉格朗日乘子。
设yk=[x1k; x2k; x3k; (λk)T]∈
| $\begin{array}{l} \left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{a}}_1^{\rm{T}}{\mathit{\boldsymbol{a}}_1}} & 0 & 0 & 0\\ {\mathit{\boldsymbol{a}}_2^{\rm{T}}{\mathit{\boldsymbol{a}}_1}} & {\mathit{\boldsymbol{a}}_2^{\rm{T}}{\mathit{\boldsymbol{a}}_2}} & 0 & 0\\ {\mathit{\boldsymbol{a}}_3^{\rm{T}}{\mathit{\boldsymbol{a}}_1}} & {\mathit{\boldsymbol{a}}_3^{\rm{T}}{\mathit{\boldsymbol{a}}_2}} & {\mathit{\boldsymbol{a}}_3^{\rm{T}}{\mathit{\boldsymbol{a}}_3}} & 0\\ {{\mathit{\boldsymbol{a}}_1}} & {{\mathit{\boldsymbol{a}}_2}} & {{\mathit{\boldsymbol{a}}_3}} & {{\mathit{\boldsymbol{I}}_{3 \times 3}}} \end{array}} \right]{\mathit{\boldsymbol{y}}^{k + 1}} = \\ \left[ {\begin{array}{*{20}{l}} 0 & { - \mathit{\boldsymbol{a}}_1^{\rm{T}}{\mathit{\boldsymbol{a}}_2}} & { - \mathit{\boldsymbol{a}}_1^{\rm{T}}{\mathit{\boldsymbol{a}}_3}} & {\mathit{\boldsymbol{a}}_1^{\rm{T}}}\\ 0 & 0 & { - \mathit{\boldsymbol{a}}_2^{\rm{T}}{\mathit{\boldsymbol{a}}_3}} & {\mathit{\boldsymbol{a}}_2^{\rm{T}}}\\ 0 & 0 & 0 & {\mathit{\boldsymbol{a}}_3^{\rm{T}}}\\ 0 & 0 & 0 & {{\mathit{\boldsymbol{I}}_{3 \times 3}}} \end{array}} \right]{\mathit{\boldsymbol{y}}^k} + \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{b}}}\\ {\;\;\mathit{\boldsymbol{b}}} \end{array}} \right] \end{array}$ | (11) |
定义
| $\begin{align} & \mathit{\boldsymbol{L}}=\left[ \begin{array}{*{35}{l}} \mathit{\boldsymbol{a}}_{1}^{\rm{T}}{{\mathit{\boldsymbol{a}}}_{1}} & 0 & 0 \\ \mathit{\boldsymbol{a}}_{2}^{\rm{T}}{{\mathit{\boldsymbol{a}}}_{1}} & \mathit{\boldsymbol{a}}_{2}^{\rm{T}}{{\mathit{\boldsymbol{a}}}_{2}} & 0 \\ \mathit{\boldsymbol{a}}_{3}^{\rm{T}}{{\mathit{\boldsymbol{a}}}_{1}} & \mathit{\boldsymbol{a}}_{3}^{\rm{T}}{{\mathit{\boldsymbol{a}}}_{2}} & \mathit{\boldsymbol{a}}_{3}^{\rm{T}}{{\mathit{\boldsymbol{a}}}_{3}} \\ \end{array} \right] \\ & \mathit{\boldsymbol{R}}=\left[ \begin{array}{*{35}{l}} 0 & -\mathit{\boldsymbol{a}}_{1}^{\rm{T}}{{\mathit{\boldsymbol{a}}}_{2}} & -\mathit{\boldsymbol{a}}_{1}^{\rm{T}}{{\mathit{\boldsymbol{a}}}_{3}} \\ 0 & 0 & -\mathit{\boldsymbol{a}}_{2}^{\rm{T}}{{\mathit{\boldsymbol{a}}}_{3}} \\ 0 & 0 & 0 \\ \end{array} \right] \\ \end{align}$ |
则L和R的关系为:L-R=ATA,其中A为Ax=y的系数矩阵。
定义
| $\mathit{\boldsymbol{\bar L = }}\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{L}} & 0\\ \mathit{\boldsymbol{A}} & {{\mathit{\boldsymbol{I}}_{3 \times 3}}} \end{array}} \right],\mathit{\boldsymbol{\bar R = }}\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{R}} & {{\mathit{\boldsymbol{A}}^{\rm{T}}}}\\ 0 & {{\mathit{\boldsymbol{I}}_{3 \times 3}}} \end{array}} \right],\mathit{\boldsymbol{\bar b}} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{b}}}\\ {\;\;\mathit{\boldsymbol{b}}} \end{array}} \right],$ |
则式(10) 可写为
| ${\mathit{\boldsymbol{y}}^{k + 1}} = {\left( {\mathit{\boldsymbol{\bar L}}} \right)^{ - 1}}\mathit{\boldsymbol{\bar R}}{\mathit{\boldsymbol{y}}^k} + {{\mathit{\boldsymbol{\bar L}}}^{ - 1}}\mathit{\boldsymbol{\bar b}}$ |
因为ρ((L)-1R)>1[10](ρ(·)表示谱半径),即谱半径大于1,所以ADMM对于式(6) 并不收敛。
2) 应用RP-ADMM求解式(6),当迭代到第k次时其格式变为
| ${\mathit{\boldsymbol{y}}^{k + 1}} = {{\mathit{\boldsymbol{\bar L}}}^{ - 1}}_\sigma {{\mathit{\boldsymbol{\bar R}}}_\sigma }{\mathit{\boldsymbol{y}}^k} + {{\mathit{\boldsymbol{\bar L}}}^{ - 1}}_\sigma \mathit{\boldsymbol{\bar b}}$ |
其中σ∈Γ={σ|序列(1, 2, 3) 的随机排序}
引理1[11] 假设A=[A1, …, An]∈
| $M = {E_\sigma }({{\mathit{\boldsymbol{\bar L}}}^{ - 1}}_\sigma {{\mathit{\boldsymbol{\bar R}}}_\sigma }) = \frac{1}{{n!}}\sum\limits_{\sigma \in \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}} {({{\mathit{\boldsymbol{\bar L}}}^{ - 1}}_\sigma {{\mathit{\boldsymbol{\bar R}}}_\sigma })} $ |
因为Γ中的变量是服从均匀随机变量的,所以E是关于Γ的期望。因此ρ(M)<1。
综合1) 和2) 的结果,得出M的谱半径小于1,证明RP-ADMM算法是收敛的,结论得证。
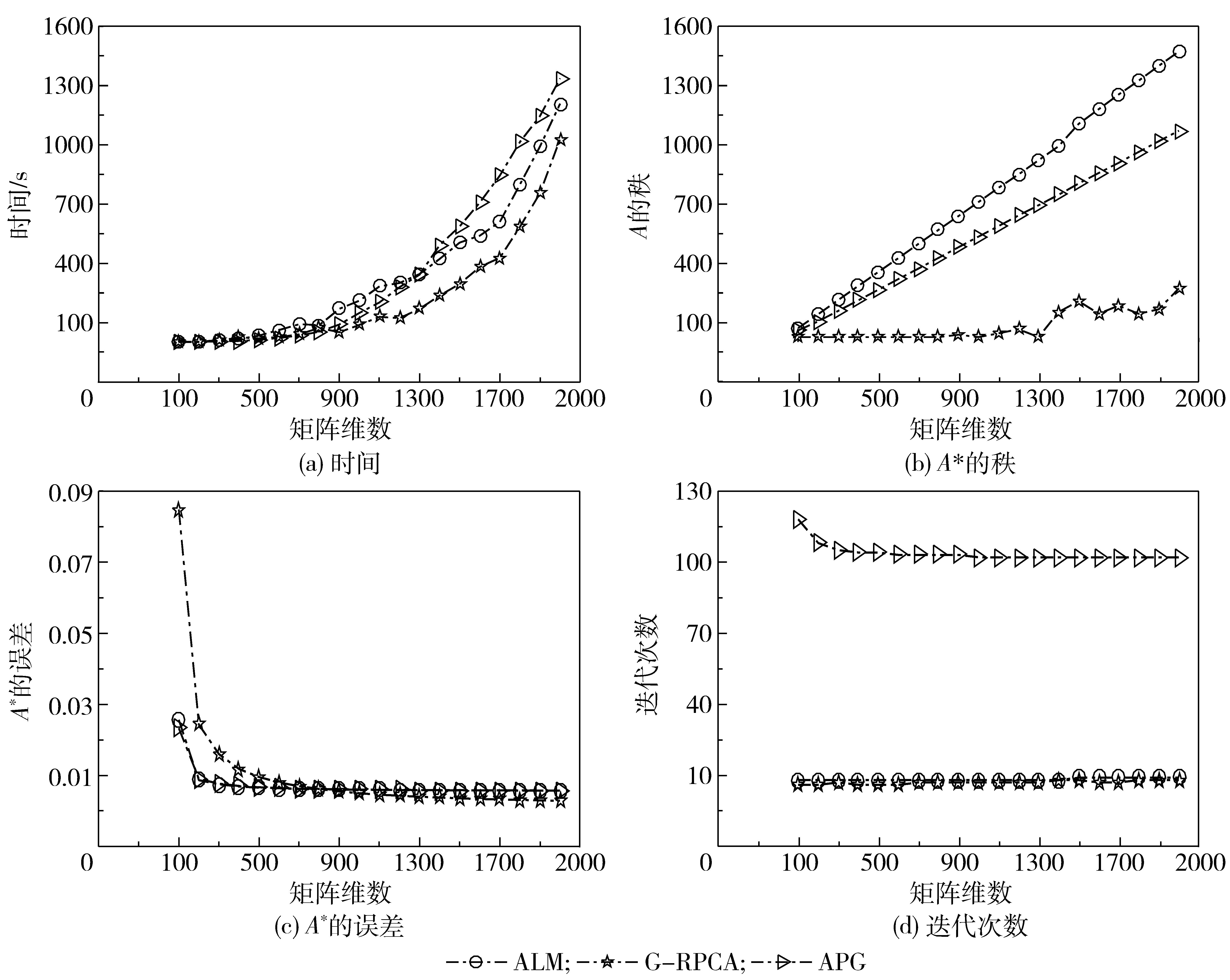
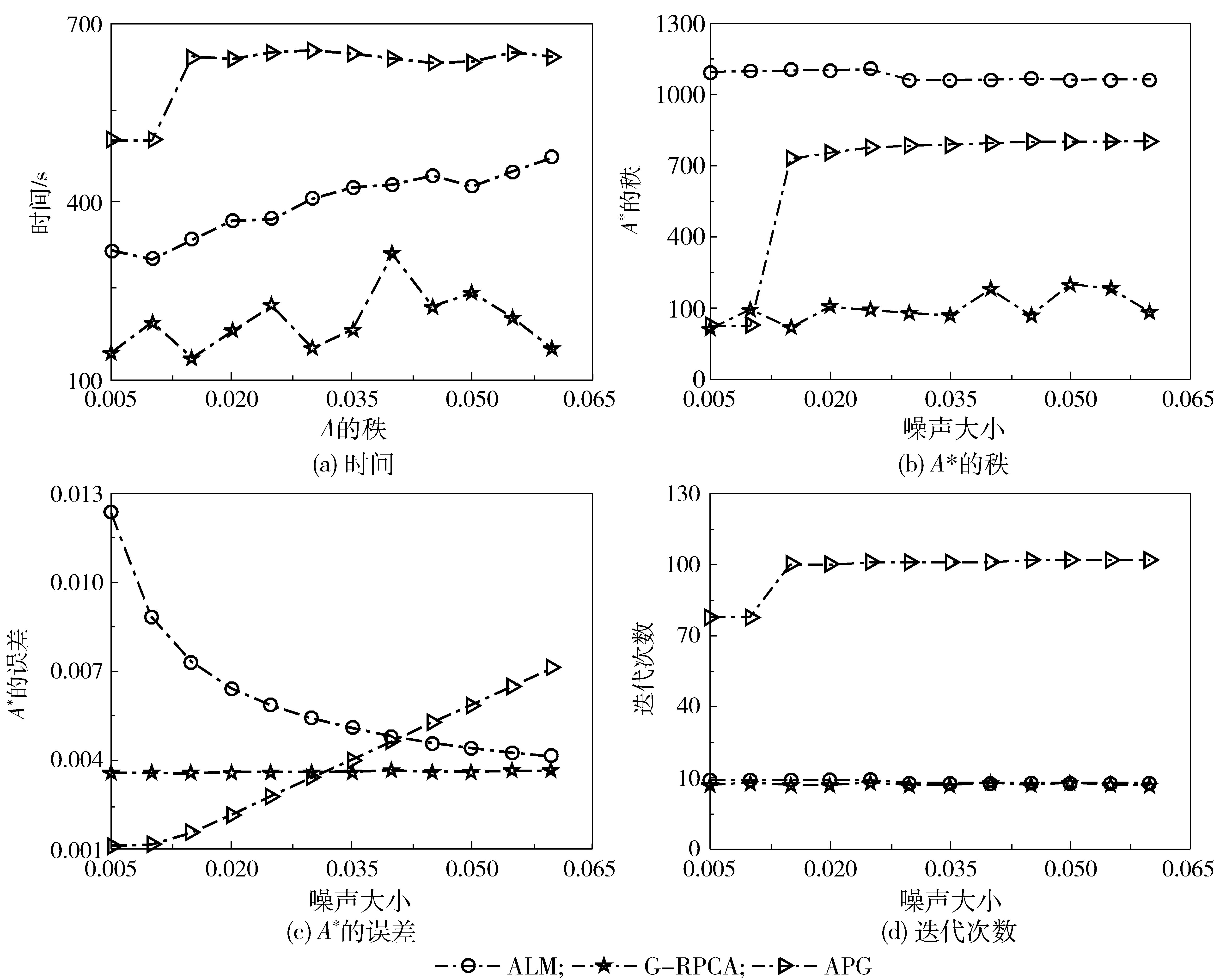
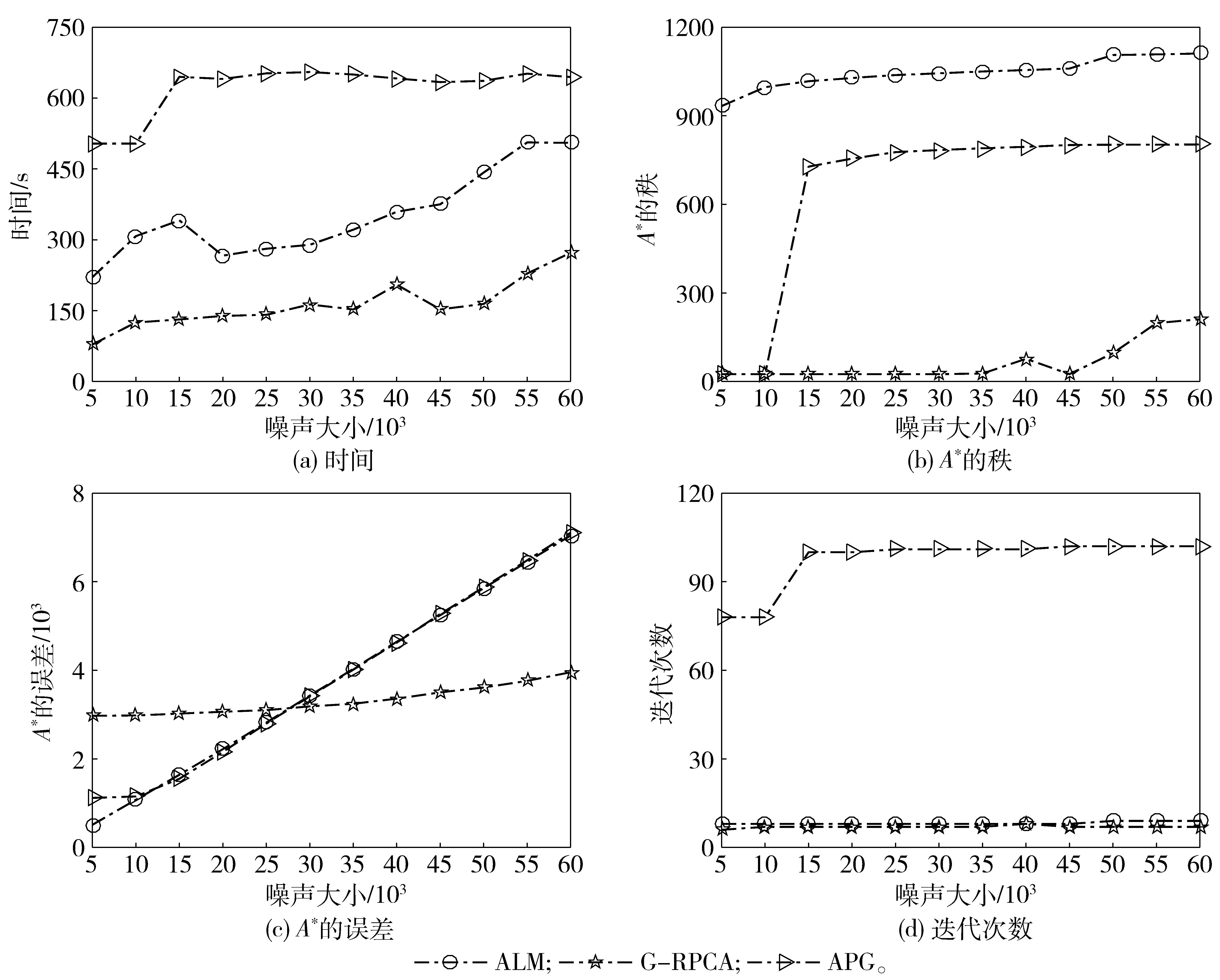
2 数值模拟为测试G-RPCA模型分离稀疏大噪声和稠密小噪声的能力,采用n阶方阵作测试。低秩矩阵A∈Rn×n可由元素服从i.i.d标准正态分布的两个独立随机矩阵MLn×r和MRn×r的乘积产生;稀疏大误差矩阵E∈Rn×n的支集元素在区间[-500, 500]上随机均匀取值;致密的高斯小噪声矩阵N∈Rn×n的元素服从i.i.d标准正态分布。由此可得到受稀疏大噪声和稠密小噪声污染的矩阵D=A+E+σN(σ=0.001)(F=σN)。分别改变矩阵D的维数(m=100:100:2000)、低秩矩阵A的秩(rank(A)=5:5:60) 和高斯噪声的大小(σ=0.005:0.005:0.06),得到G-RPCA、ALM和APG这3种算法的性能比较。图 1为设定高斯噪声0.05和低秩矩阵的秩15,改变矩阵维数的结果;图 2为设定矩阵维数1500阶和高斯噪声0.05,改变低秩矩阵的秩的结果;图 3为设定矩阵维数1500阶和低秩矩阵的秩15,改变高斯噪声的结果。
|
图 1 不同矩阵维数下3种算法的性能比较 Fig.1 Performance comparison of three algorithms with different matrix dimensions |
|
图 2 改变低秩矩阵的秩时3种算法的性能比较 Fig.2 Performance comparison of three algorithms when changing the rank of the lower rank matrix |
|
图 3 不同噪声值下3种算法的性能比较 Fig.3 Performance comparison of three algorithms with different noise |
从图 1中可以看出,随着矩阵维数的增加,低秩部分的秩并没有显著的变化,这说明G-RPCA模型所恢复出的低秩部分鲁棒性很好。在图 2和图 3中,不管是随着噪声的增大还是矩阵秩的改变,G-RPCA模型所恢复出的矩阵相对于其他算法都更加鲁棒且其迭代次数也更少。
3 含有混合噪声的图像分离任选一幅图像对其添加混合噪声,然后分别应用G-RPCA方法和ALM方法去噪,结果如图 4、5所示。

|
图 4 G-RPCA图像去噪 Fig.4 G-RPCA image denoising |

|
图 5 ALM图像去噪 Fig.5 ALM image denoising |
对比图 4、5可以明显看出,G-RPCA去除噪后的图片比ALM更清晰,说明G-RPCA方法能有效分离出稠密的小噪声。
4 结束语本文对于G-RPCA模型基于随机排序的交替方向乘子法提出一种可行的求解方法。通过数值实验可以表明该算法在处理混合噪声问题上,无论从时间成本还是从所恢复出的低秩矩阵秩的鲁棒性上都优于其他两种通用的算法。图像实例也证明了该算法能够分别分离出稀疏大噪声和稠密的小噪声,在去除混合噪声方面具有一定优势。
| [1] |
Wright J, Peng Y G, Ma Y. Robust principal component analysis:exact recovery of corrupted low-rank matrices via convex optimization[C]//Twenty-Third Annual Conference on Neural Information Processing Systems. Vancouver, Canada, 2009:2080-2088.
|
| [2] |
Candès E J, Li X D, Ma Y, et al. Robust principal component analysis?[J]. Journal of the ACM, 2011, 58(3): 11-48. |
| [3] |
Xu H, Caramanis C, Sanghavi S. Robust PCA via outlier pursuit[C]//Twenty-Third Annual Conference on Neural Information Processing Systems. Vancouver, Canada, 2010:2496-2504.
|
| [4] |
Candès E J, Tao T. The power of convex relaxation:near-optimal matrix completion[J]. IEEE Transactions on Information Theory, 2010, 56(1): 2053-2080. |
| [5] |
Candès E J, Recht B. Exact matrix completion via convex optimization[J]. Foundations of Computational Mathematics, 2009, 9(2): 717-772. |
| [6] |
Lin Z C, Ganesh A, Wright J, et al. Fast convex optimization algorithms for exact recovery of a corrupted low-rank matrix[J]. Journal of the Marine Biological Association of the United Kingdom, 2009, 56(3): 707-722. |
| [7] |
Lin Z C, Chen M M, Ma Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices[J]. Journal of the Marine Biological Association of the United Kingdom, 2010, 55(3): 607-626. |
| [8] |
Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends in Machine Learning, 2010, 3(1): 1-122. DOI:10.1561/2200000016 |
| [9] |
Xie W S, Yang Y F, Zhou B. An ADMM algorithm for second-order TV-based MR image reconstruction[J]. Numerical Algorithms, 2014, 67(4): 827-843. DOI:10.1007/s11075-014-9826-z |
| [10] |
Chen C H, He B S, Ye Y Y, et al. The direct extension of ADMM for multi-block convex minimization problems is not necessarily convergent[J]. Mathematical Programming, 2016, 155(1): 57-79. |
| [11] |
Sun D, Toh K C, Yang L. A convergent 3-block semi-proximal alternating direction method of multipliers for conic programming with 4-type of constraints[J]. Society for Industrial and Applied Mathematic, 2015, 25(2): 882-915. |








