2. 中国科学院高能物理研究所, 北京 100049;
3. 中国石油塔里木油田分公司, 新疆 库尔勒 841000
2. Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049;
3. Petro China Tarim Oilfield Company, Korla, Xinjiang 841000, China
滚动轴承是旋转机械中应用广泛的部件之一,其寿命过短将影响设备的正常运转。准确预测滚动轴承寿命可以合理安排其性能检查及维护更换工作,避免停车过早影响生产进程或停车过晚造成设备损坏。
滚动轴承寿命预测主要有基于统计模型、基于断裂力学模型和基于数据驱动模型3种方法[1]。基于统计模型的方法是应用数理统计的原理分析滚动轴承寿命[2],利用观测数据及失效机理建立以可靠性为基础的统计公式,可解决寿命计算中参数不易获取的问题;但在实际应用中存在计算结果较分散、数据不易获取的缺点。基于断裂力学模型的方法假定滚动轴承的失效过程符合裂纹扩展规律,并据此建立裂纹扩展模型[3]来预测滚动轴承寿命;但该方法需要大量的专家经验及较复杂的故障机理知识,实现预测难度较大,且采用单一模型,致使退化规律描述不足。基于数据驱动的方法利用滚动轴承运行状态信息分析滚动轴承寿命[4],适合解决滚动轴承运行过程中物理规律复杂、不确定因素较多的情况,在实际应用中可依据滚动轴承运行状态作实时调整;其缺点是没有考虑故障机理问题,滚动轴承退化规律不明确,参数影响较大。
如何应用少量的运行状态信息建立准确的滚动轴承寿命预测物理模型,并实现实时准确地预测滚动轴承寿命是目前滚动轴承寿命预测中面临的难题,因此本文提出基于状态监测信息和滚动轴承退化物理模型的寿命预测方法,利用滚动轴承运行状态信息对滚动轴承不同退化阶段理论公式进行改进,构建不同退化阶段状态空间模型,保证滚动轴承预测退化趋势的可靠性;为实现实时准确预测滚动轴承寿命,对已建立的状态空间模型进行参数调整,确保模型能够更好描述滚动轴承退化趋势,并应用粒子滤波算法进行滚动轴承寿命预测,保证预测过程能依据实际运行状态实时调整,提高寿命预测的准确性。
1 模型及算法 1.1 状态空间模型动态状态空间模型主要由两种方程组成:一是状态方程,反映某时间点动态系统在输入变量影响下所转移到的状态,这种状态描述了系统的内部状况,是系统的本质变化;二是观测方程,它将系统在某时间点的状态以某种形式输出,反映了系统内部随输入变量变化而呈现出的变化。
通常定义状态空间模型如下:
动态模型
观测模型
其中ft和ht均是非线性函数;wt是过程噪声,vt是观测噪声,二者是互相不影响且没有关联的噪声序列[5]。
状态空间模型将状态变量并入可观测模型,并利用其得到估计结果;同时它能够用最少信息形式描述系统的状态,即只需利用少量历史数据资料就可进行运算,节省了运算时间。
1.2 粒子滤波算法粒子滤波算法(particle filter,PF)在贝叶斯估计理论的基础之上对蒙特卡洛方法进行了改进,主要应用粒子样本表示概率的数值变化情况。粒子滤波算法应用状态方程描绘系统的动态变化情况,应用观测方程描绘当前系统的输出信号,同时还能处理非高斯非线性的多维信号,很大程度上解决了状态空间方法计算难度大的问题。
粒子滤波算法包括粒子产生、重要性采样、权重更新、重采样、状态估计5个步骤[6],具体如下。
(1) 粒子集初始化 令k=0,应用先验概率分布p(x0)生成采样粒子{x0(i)}i=1N,wo(i)=1/N,其中p(x0)为先验密度的初始值;
(2) 重要性采样 计算样本集的累计权值
(3) 权重更新计算粒子重要性权重和归一化权重
| $\begin{array}{l} w_k^{(i)} = w_{k - 1}^{(i)}\frac{{p({y_k}|\tilde x_k^{(i)})p(\tilde x_k^{(i)}|\tilde x_{k - 1}^{(i)}){\rm{ }}}}{{q(\tilde x_k^{(i)}|\tilde x_{0:k - 1}^{(i)},{y_{1:k}})}}\\ w_k^{(i)} = \frac{{w_k^{(i)}}}{{\sum\limits_{j = 1}^N {w_k^{(i)}} }} \end{array}$ |
其中,p(yk|xk)为系统状态的观测似然概率密度,p(xk|xk-1)为系统的状态转移概率密度;
(4) 重采样 计算有效样本
(5) 状态估计
首先针对滚动轴承不同退化阶段分别建立状态空间模型,然后对已建立模型参数进行调整,同时应用粒子滤波算法递推预测寿命。
2.1 不同退化阶段状态空间模型的建立针对滚动轴承物理模型难建立、模型单一的问题,对滚动轴承不同退化阶段物理公式Paris及Foreman进行改进推导,建立不同退化阶段状态空间模型。断裂力学扩展理论支持从裂纹开始扩展时刻进行预测[7],所以本文主要预测滚动轴承退化第二及第三阶段,即预测滚动轴承退化中后期。
2.1.1 退化第二阶段状态空间模型Paris公式用来描述疲劳裂纹稳定扩展规律,即裂纹扩展的第二阶段,其理论公式采用的纯物理数据较难获取和计算。常见的Paris公式为
| $\frac{{{\rm{d}}l}}{{{\rm{d}}N}} = C{(\Delta k)^n}$ | (1) |
式中,l为裂纹长度,N为应力循环次数,
裂纹的基本类型分为张开型、滑移型、反平面剪切型。由于第一种类型最常发生,所以采用第一种类型的应力强度因子公式改进计算
| $K = \sigma \sqrt {{\rm{ \mathsf{ π} }}l} $ | (2) |
式中,σ为轴承裂纹处应力。由于
| $\Delta k = {K_{{\rm{max}}}} - {K_{{\rm{min}}}}$ | (3) |
其中Kmin、Kmax分别为等幅交变载荷最小值和最大值。
由式(1)~(3) 推导得出
| $\begin{array}{l} \frac{{{\rm{d}}l}}{{{\rm{d}}N}} = C{(\sigma \sqrt {{\rm{ \mathsf{ π} }}{l_{{\rm{max}}}}} - \sigma \sqrt {{\rm{ \mathsf{ π} }}{l_{{\rm{min}}}}} )^n} = {\rm{ }}C{\sigma ^n}{\sqrt {\rm{ \mathsf{ π} }} ^n}\\ {(\sqrt {{l_{{\rm{max}}}}} - \sqrt {{l_{{\rm{min}}}}} )^n} \end{array}$ | (4) |
式中,lmin、lmax分别为裂纹长度的最小值和最大值。
由于裂纹长度l与轴承振动数据V之间呈非线性关系,即l~V,轴承裂纹处应力σ与载荷q相关,亦呈非线性关系,即σ~q,则式(4) 可推导转化为
| $\frac{{{\rm{d}}l}}{{{\rm{d}}N}} = {k_1}{q^m}{\sqrt {\rm{ \mathsf{ π} }} ^m}{({V_{{\rm{dq}}}} - {V_{{\rm{nr}}}})^m}$ | (5) |
式(5) 两边同时对N积分,得到最终公式
| $\frac{{V\left( {t + 1} \right)}}{{N - {N_{{\rm{or}}}}}} = {k_1}{q^m}{\sqrt {\rm{ \mathsf{ π} }} ^m}{({V_{{\rm{dq}}}} - {V_{{\rm{nr}}}})^m} + w\left( t \right)$ | (6) |
基于公式(6) 提出改进的第二阶段状态空间模型如式(7)、(8) 所示。
状态方程
| $\frac{{V\left( {t + 1} \right)}}{{N - {N_{{\rm{or}}}}}} = {k_1}{q^m}{\sqrt {\rm{ \mathsf{ π} }} ^m}{({V_{{\rm{dq}}}} - {V_{{\rm{nr}}}})^m} + w\left( t \right)$ | (7) |
观测方程
| $y\left( {t + 1} \right) = \frac{{V\left( {t + 1} \right)}}{{N - {N_{{\rm{or}}}}}}(N - {N_{{\rm{or}}}}) + v\left( t \right)$ | (8) |
其中,Vdq为当前轴承振动数值,Vnr为正常运转振动数值,Nor为开始退化时应力循环次数,V(t+1) 为轴承(t+1) 时刻的特征数据,w(t)为t时刻状态转移的扰动,即轴承运转过程中产生的过程噪声的值,v(t)为t时刻轴承运转过程中产生的观测噪声的值,y(t+1) 即为最终状态预测值,k1、m是材料系数,依据材料特性和实验环境发生变化。
2.1.2 退化第三阶段状态空间模型由于滚动轴承寿命预测大多针对第二阶段而疏忽裂纹迅速扩展的第三阶段,使得预测结果误差相应增大。第三阶段裂纹扩展规律由Foreman公式来描述
| $\frac{{{\rm{d}}l}}{{{\rm{d}}N}} = \frac{{C{{(\Delta k)}^m}}}{{\left( {1 - R} \right){K_{\rm{c}}} - \Delta k}}$ | (9) |
式中,Kc为材料的断裂韧性,R为应力比值,且
| $R = \frac{{{K_{{\rm{min}}}}}}{{{K_{{\rm{max}}}}}}$ | (10) |
当Kmax→Kc时,裂纹扩展速率快速增加。由式(9)、(10) 推导得出
| $\begin{array}{l} \left( {1 - R} \right){K_{\rm{c}}} - \Delta k = \left( {1 - \frac{{{K_{{\rm{min}}}}}}{{{K_{{\rm{max}}}}}}} \right){K_{\rm{c}}} - \Delta k = \\ \Delta k\left( {\frac{{{K_{\rm{c}}} - {K_{{\rm{min}}}}}}{{{K_{{\rm{max}}}}}}} \right) \end{array}$ |
由于K值与受力相关,而振动数值可以体现受力,设定Ved为振动停车阈值,Vmax为目前采集到的振动数据最大值,即Vmax=x(t),则式(9) 变换为
| $\frac{{{\rm{d}}l}}{{{\rm{d}}N}} = \frac{{C{{(\Delta k)}^m}}}{{\left( {1 - R} \right){K_{\rm{c}}} - \Delta k}} = = \frac{{C{{(\Delta k)}^m}}}{{\Delta k}}\left( {\frac{{{K_{{\rm{max}}}}}}{{{K_{\rm{c}}} - {K_{{\rm{max}}}}}}} \right)$ | (11) |
由于K=σ
| $\frac{{{K_{{\rm{max}}}}}}{{{K_{\rm{c}}} - {K_{{\rm{max}}}}}} \sim \frac{{{V_{{\rm{max}}}}}}{{{V_{{\rm{ed}}}} - {V_{{\rm{max}}}}}}$ | (12) |
将式(12) 中的Vmax用x(t)替代,同时对式(11) 中N积分,则得到
| $\frac{{x\left( {t + 1} \right)}}{{N - {N_{{\rm{or}}}}}} = x\left( t \right)\frac{{{k_1}{q^m}{{\sqrt {\rm{ \mathit{ π} }} }^m}{{({V_{{\rm{dq}}}} - {V_{{\rm{nr}}}})}^m} + w\left( t \right)}}{{{V_{{\rm{ed}}}} - x\left( t \right)}}{V_{{\rm{ed}}}}$ | (13) |
依据式(13) 提出第三阶段状态空间模型如式(14)、(15) 所示。
状态方程
| $\begin{array}{l} \frac{{V\left( {t + 1} \right)}}{{N - {N_{{\rm{or}}}}}} = ({k_1}{q^m}{\sqrt {\rm{ \mathsf{ π} }} ^m}{({V_{{\rm{dq}}}} - {V_{{\rm{nr}}}})^m} + w\left( t \right))\\ \frac{{x\left( t \right)}}{{{V_{{\rm{ed}}}} - x\left( t \right)}} \end{array}$ | (14) |
观测方程
| $y\left( {t + 1} \right) = \frac{{V\left( {t + 1} \right)}}{{N - {N_{{\rm{or}}}}}}(N - {N_{{\rm{or}}}}) + v\left( t \right)$ | (15) |
式中,Ved为振动停车阈值,其余参数同第二阶段状态空间模型。
不同退化阶段状态空间模型方法将疲劳、断裂力学模型方法及数据驱动方法结合,同时解决了预测模型单一导致的预测轨迹偏差较大的问题,提高了预测结果的准确性。
2.2 基于粒子滤波的滚动轴承预测采用2.1节建立的不同退化阶段状态空间模型描述滚动轴承退化趋势,并用粒子滤波算法递推预测滚动轴承特征值趋势,计算滚动轴承寿命,具体步骤如下:
1) 获取受力载荷,采集滚动轴承运行状态信息,从中提取特征值;
2) 设置报警阈值、退化第三阶段阈值及停车阈值分别为预测初始点,退化第二、三阶段分界点及预测截止点;设置报警阈值为区域B上限的1.25倍,退化第三阶段阈值为区域C上限数值,停车阈值为区域C上限的1.25倍[8];
3) 当特征值大于等于报警阈值时,开始滚动轴承寿命预测;
4) 设置粒子滤波算法初始值;
5) 设置预测步长为10,建立不同退化阶段状态空间模型,依据文献[9]及式(5),设置状态空间模型材料常数k1和m的初始值分别为1×10-3和0.1;
6) 每隔3 h取预测时刻前20个特征值作为输入数据;
7) 当特征值小于等于第三阶段阈值时,应用非线性最小二乘法更新第二阶段模型参数,以形成符合实际运行状态的退化第二阶段状态空间模型;反之,应用非线性最小二乘法更新第三阶段模型参数,形成符合实际运行状态的退化第三阶段状态空间模型;
8) 利用状态空间模型及粒子滤波算法预测特征值趋势;
9) 当预测特征值小于停车阈值时,循环递推预测特征值趋势;反之则输出预测时刻的滚动轴承寿命。
3 实验及数据分析 3.1 实验数据采集和特征参数提取利用美国辛辛那提大学IMS实验室的滚动轴承全寿命周期振动实验数据[10],选取其中第一组样本数据中的内圈故障数据进行分析;该实验持续34天11时40分,为确保滚动轴承运行稳定,使用其前32天数据,并剔除严重退化点之后的数据。
考虑滚动轴承类型多样、退化机理形式复杂等情况,本文以疲劳剥落故障形式为主研究滚动轴承寿命,即主要研究滚动轴承处于正常工况下的寿命,具体过程如下。
通过对采集到的数据应用小波包能量提取方法[11]计算不同时刻的特定频带能量,得出能量冲击在2 kHz以下表现明显;利用切比雪夫滤波器以2 kHz为分界点得到滚动轴承的高频信号及低频信号,同时针对低频信号提取方差、峰峰值、波形指标、峰值指标、脉冲指标、裕度指标、偏斜度指标、峭度指标、加速度有效峰值、包络谱峰值等10个特征指标;通过特征评估算法[12]得出包络谱峰值对于滚动轴承退化过程反应灵敏,并将其作为滚动轴承寿命预测特征值。
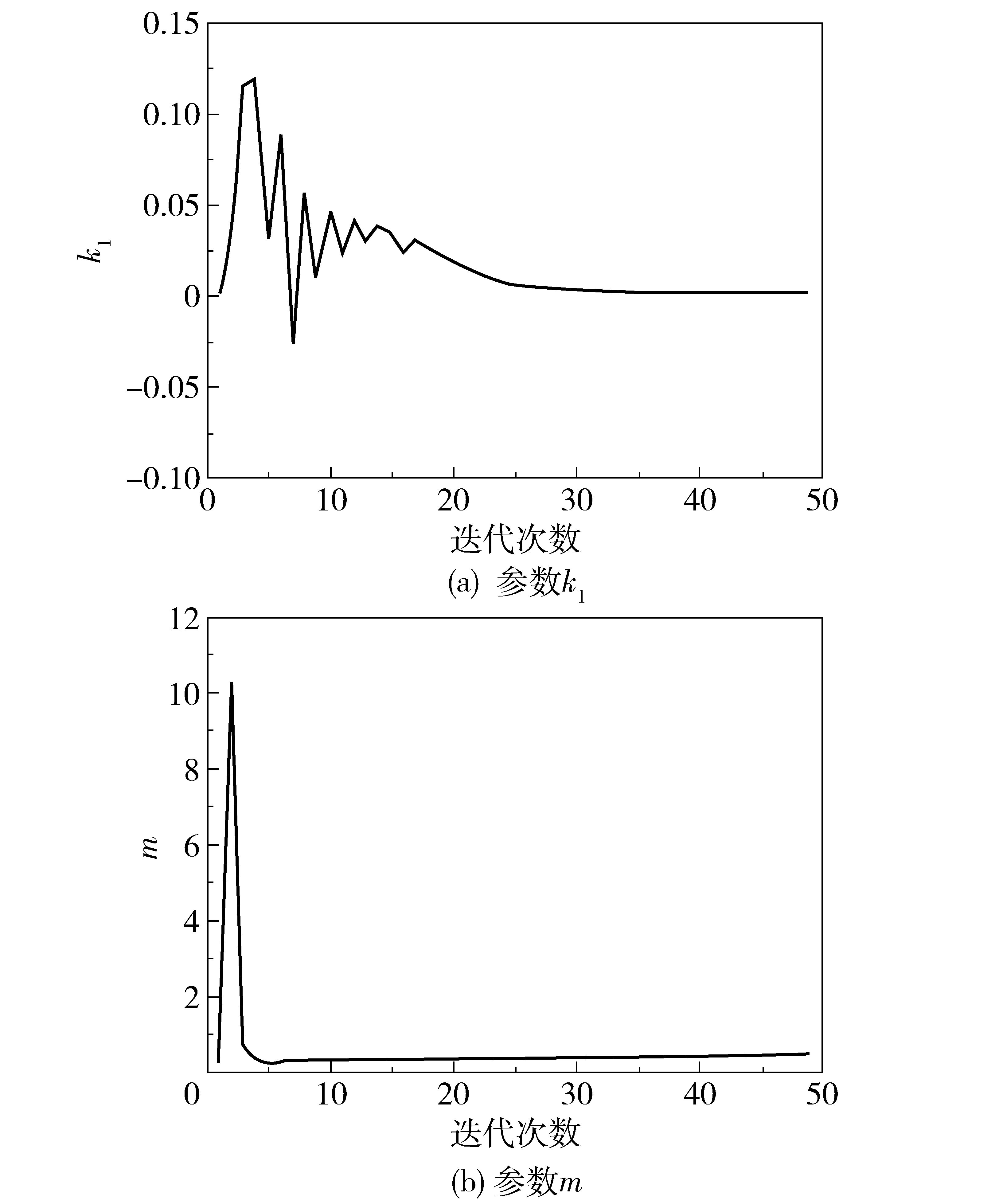
3.2 预测结果分析将包络谱峰值(A)归一化,设置报警阈值、退化第三阶段阈值、停车阈值分别为3.0 m/s2、7.0 m/s2、9.0 m/s2[8];取k1初始值为1×10-3,m初始值为0.1,噪声w(t)及v(t)按照正态分布选取。为避免权重值影响过大,设权重取值区间为(0, 1)。当A大于等于报警阈值时,按2.2节所示步骤进行滚动轴承寿命预测。应用非线性最小二乘法调整模型参数,参数收敛过程如图 1所示。
|
图 1 模型参数收敛过程 Fig.1 Model parameter convergence process |
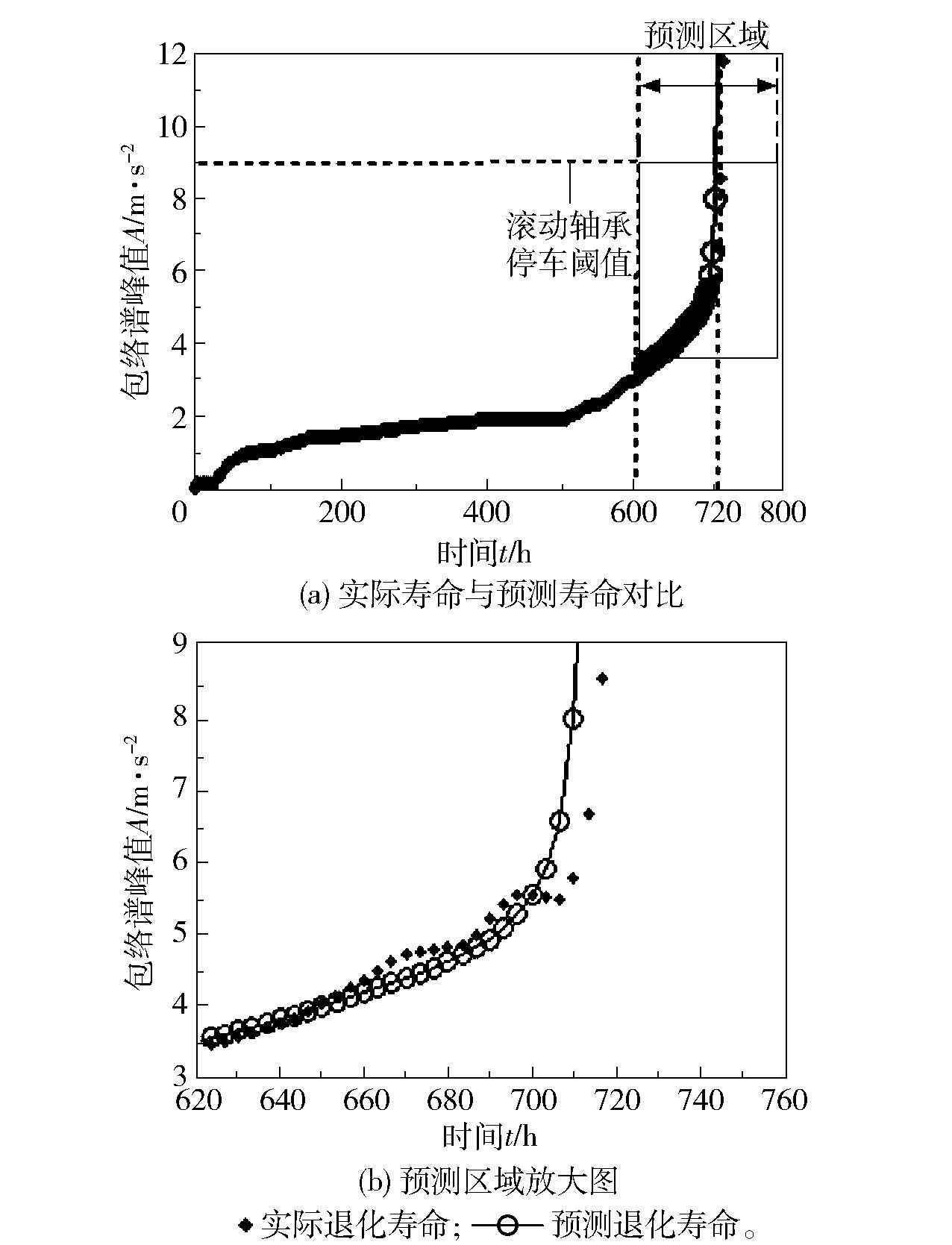
模型参数调整后,利用不同退化阶段状态空间模型及粒子滤波算法进行滚动轴承寿命预测,结果如图 2(a)所示,图(b)为(a)中预测区域放大图。
|
图 2 滚动轴承寿命预测结果 Fig.2 Rolling bearing life prediction result |
由图 2可知,基于不同退化阶段状态空间模型及粒子滤波的滚动轴承寿命预测方法能较为准确地反映滚动轴承退化过程,寿命预测退化曲线与实际退化曲线较接近,表明该方法具有一定可行性。
为检验模型参数定时调整后不同退化阶段状态空间模型的有效性,沿滚动轴承退化轨迹进行不同时刻滚动轴承寿命预测,预测结果如表 1所示。
| 下载CSV 表 1 不同预测时刻实际寿命与预测寿命误差对比 Table 1 Error comparisons of actual life and predicted life for different prediction times |
由表 1可知,随着预测时间点向后推移,预测误差逐渐减小。主要是由于随着滚动轴承运行状态的改变,模型参数定时调整,及时纠正了模型运行轨迹,使模型预测退化趋势与实际退化趋势相吻合。在预测过程中,只需输入预测时刻点前2~3天的实验数据,大大节省了预测时间,减少了计算量。
3.3 寿命预测效果评估为验证不同退化阶段状态空间模型在滚动轴承寿命预测中的优势,选取Gamma模型[13]与退化第二阶段模型作对比。同时选用均方根误差(RMSE)、平均绝对误差(MAE)、方差绝对误差(VAE)、平均相对误差(MARE)和方差相对误差(VRE)[13]对3种方法的预测效果进行综合评估,结果如表 2所示。
| 下载CSV 表 2 3种寿命预测方法的预测结果评估 Table 2 Evaluation of different models of life prediction results |
通过表 2对比得出,不同退化阶段状态空间模型寿命预测方法较退化第二阶段模型及Gamma模型在准确度和精确度方面均有较大提高,整体预测效果更佳。这主要是由于不同退化阶段状态空间模型包含了滚动轴承退化的第二及第三阶段,预测退化轨迹与实际退化轨迹接近,使改进后的模型能更准确地反映滚动轴承的退化过程;而Gamma模型主要基于概率方法,计算结果与先验概率分布相关,与滚动轴承退化机理相关性较小。
4 结论(1) 本文提出的基于不同退化阶段状态空间模型及粒子滤波的滚动轴承寿命预测方法结合了断裂力学模型及数据驱动两种方法,有效解决了滚动轴承物理退化模型难建立、全寿命数据有限带来的寿命预测结果准确性较低的问题。
(2) 通过实验评估结果得出,基于不同退化阶段状态空间模型及粒子滤波的滚动轴承寿命预测方法优于单一模型、粒子滤波及二者相结合的预测方法,提高了预测结果的准确性,为滚动轴承寿命预测提供了一种新的更有效的手段。
| [1] |
张小丽, 王保建, 马猛, 等. 滚动轴承寿命预测综述[J]. 机械设计与制造, 2015(10): 221-224. Zhang X L, Wang B J, Ma M, et al. A review of life prediction for roller bearing[J]. Machinery Design & Manufacture, 2015(10): 221-224. (in Chinese) DOI:10.3969/j.issn.1001-3997.2015.10.057 |
| [2] |
Ali J B, Chebel-Morello B, Saidi L, et al. Accurate bearing remaining useful life prediction based on Weibull distribution and artificial neural network[J]. Mechanical Systems & Signal Processing, 2015, 56/57: 150-172. |
| [3] |
Li Y, Kurfess T R, Liang S Y. Stochastic prognostics for rolling element bearings[J]. Mechanical Systems and Signal Processing, 2000, 14(5): 747-762. DOI:10.1006/mssp.2000.1301 |
| [4] |
申中杰, 陈雪峰, 何正嘉, 等. 基于相对特征和多变量支持向量机的滚动轴承剩余寿命预测[J]. 机械工程学报, 2013, 49(2): 183-189. Shen Z J, Chen X F, He Z J, et al. Remaining life predictions of rolling bearing based on relative features and multivariable support vector machine[J]. Journal of Mechanical Engineering, 2013, 49(2): 183-189. (in Chinese) |
| [5] |
Tanizaki H. Nonlinear and non-Gaussian state space modeling using sampling techniques[J]. Annals of the Institute of Statistical Mathematics, 2001, 53(1): 63-81. DOI:10.1023/A:1017916420893 |
| [6] |
Orchard M E, Vachtsevanos G J. A particle-filtering approach for on-line fault diagnosis and failure prognosis[J]. Transactions of the Institute of Measurement & Control, 2009, 31(3/4): 221-246. |
| [7] |
张小丽, 陈雪峰, 李兵, 等. 机械重大装备寿命预测综述[J]. 机械工程学报, 2011, 47(11): 100-116. Zhang X L, Chen X F, Li B, et al. Review of life prediction for mechanical major equipments[J]. Journal of Mechanical Engineering, 2011, 47(11): 100-116. (in Chinese) |
| [8] |
Mechanical vibration-evaluation of machine vibration by measurements on non-rotating parts-Part 7:rotodynamic pumps for industrial applications, including measurements on rotating shafts:ISO 10816-3-2009[S]. Geneva, Switzerland:International Organization for Standardization, 2009.
|
| [9] |
曲先强, 马永亮, 崔洪斌, 等. Paris公式中材料参数的统计特性分析[C]//2008全国MTS断裂测试研讨会. 成都, 2008: 26-31. Qu X Q, Ma Y L, Cui H B, et al. Statistical research of material coefficient in Paris law[C]//2008 National Seminar of MTS Fracture Test. Chengdu, 2008:26-31. (in Chinese) |
| [10] |
Qiu H, Lee J, Lin J, et al. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics[J]. Journal of Sound and Vibration, 2006, 289(4/5): 1066-1090. |
| [11] |
Hu Q, He Z J, Zhang Z S, et al. Fault diagnosis of rotating machinery based on improved wavelet package transform and SVMs ensemble[J]. Mechanical Systems and Signal Processing, 2008, 21(2): 688-705. |
| [12] |
雷亚国, 何正嘉, 訾艳阳, 等. 基于特征评估和神经网络的机械故障诊断模型[J]. 西安交通大学学报, 2006, 40(5): 558-562. Lei Y G, He Z J, Zi Y Y, et al. Mechanical fault diagnosis model based on feature evaluation and neural networks[J]. Journal of Xi'an Jiaotong University, 2006, 40(5): 558-562. (in Chinese) |
| [13] |
孙磊, 贾云献, 蔡丽影, 等. 粒子滤波参数估计方法在齿轮箱剩余寿命预测中的研究应用[J]. 振动与冲击, 2013, 32(6): 6-12. Sun L, Jia Y X, Cai L Y, et al. Residual useful life prediction of gearbox based on particle filtering parameter estimation method[J]. Journal of Vibration and Shock, 2013, 32(16): 6-12. (in Chinese) |







